The Refraction of Light and The Sun’s Position and Movement
The Refraction of Light and The Sun’s Position and Movement:
Note, the APPARENT position of celestial objects is often due to the refraction of light, which is the perturbation, and subsequent, bending of light waves as they pass through one isotropic media to another, and is contingent upon the coefficient of molecular friction, which is measured as an index of density, of the medium in which rays travel within. This phenomena is conveyed as The Index of Refraction. Thus, the APPARENT position of celestial bodies is changed due to refraction as light rays from those bodies pass through the atmosphere, and hence, we never see the ACTUAL position of any celestial events, including The Sun. We never know exactly where The Sun is or what its precise movement is. We can only observe its refracted and reflected position off The Firmament, which is, in turn. refracted again., which makes any observation of The Sun’s transit, either at the equator, or at Antarctica, a mere exercise in phantom isolation.
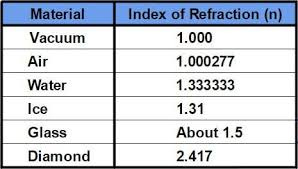
The Index of Refraction:
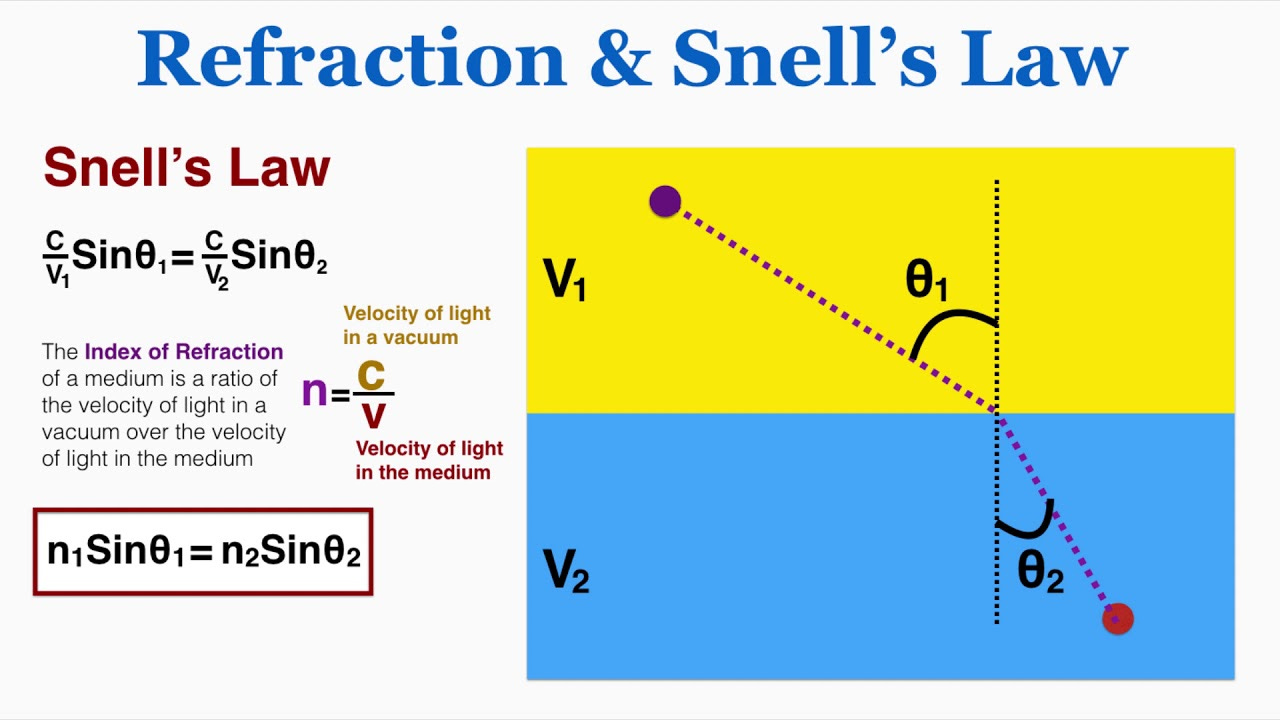
In optics, The Index of Refraction of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refracted, when entering a material. This is described by Snell's Law of Refraction, n1 sin θ1 = n2 sin θ2, where θ1 and θ2 are the angle of incidence and angle of refraction, respectively, of a ray crossing the interface between two media with refractive indices n1 and n2. The refractive indices also determine the amount of light that is reflected when reaching the interface, as well as the critical angle for total internal reflection, their intensity (Fresnel Equations) and Brewster's Angle, also known as The Polarization Angle, which is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly polarized. The angle is named after the Scottish Physicist, Sir David Brewster (1781–1868).
Snell's Law:
Snell's Law, (also known as The Snell–Descartes Law, is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index.
Example of Differential Refraction Distorting The Apparent Format of The Sun During Sunrise:
