The Moon’s Constant Trajectory Around The Earth As They Both Orbit The Sun: The Heliocentric Model Fails To Explain How The Moon Remains at a Constant Velocity
Adapted From “Pseudo-Scientific Moon Mathe-Magic” by Eric Dubay
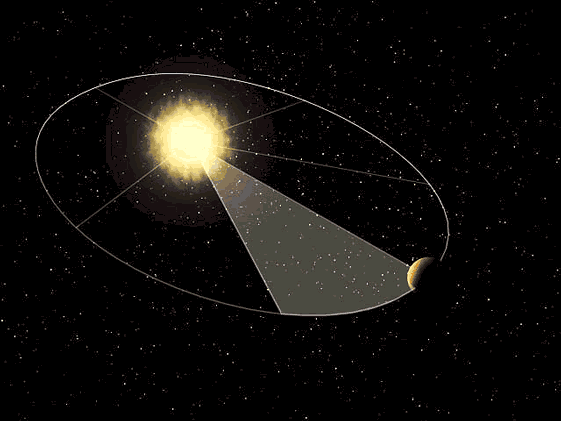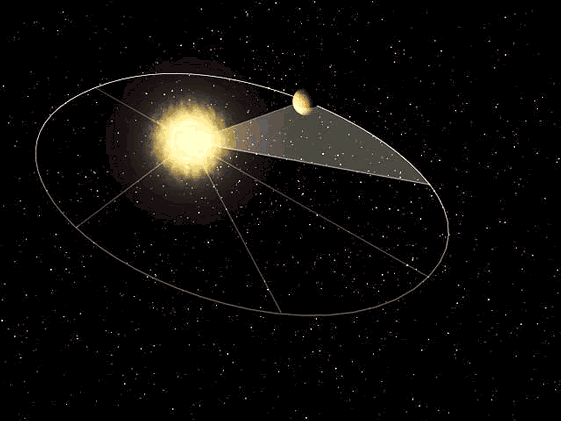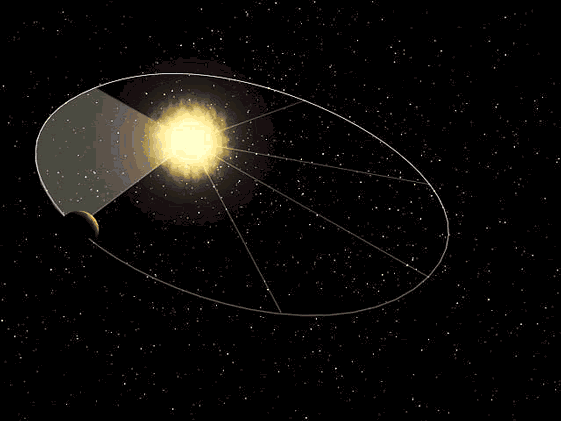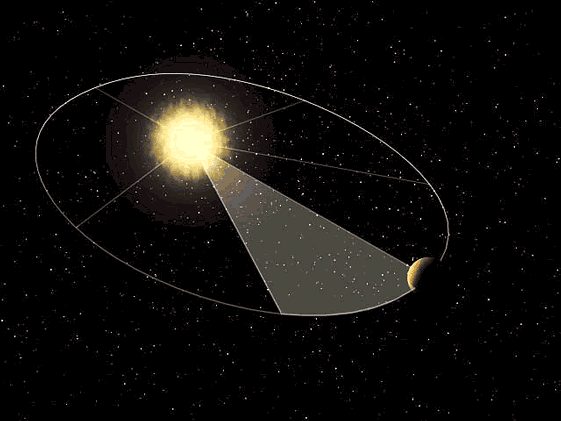
In the Heliocentric model of The Cosmos, the Moon revolves around the Earth 13 times per year, traveling at approximately 2,288 miles per hour, while the Earth revolves around the Sun once per year, traveling at approximately 66,600 miles per hour. In this model, The Moon is revolving around the Earth, which itself is revolving around the Sun, in order to maintain its regular orbit, the Moon would have to be constantly and drastically changing its speed in ways completely unaccounted for by the model. In the outer part of its orbit, the Moon would have to speed up its 66,600 miles per hour, as the Sun allegedly drags it around The Sun, in addition to its regular speed of 2,288 miles per hour, just to keep up with the Earth’s orbital speed.
And so, the Moon would then be traveling at 68,888 miles per hour when it reached the front of the Earth’s orbital path. At this point, since the Moon is allegedly 240 thousand miles away from the Earth, the Earth would catch up in just four hours, and so the Moon must continue traveling 66,600 miles per hour along Earth's trajectory while simultaneously continuing its now perpendicular 2,288 mile per hour second trajectory.
Then as it turns to reach the inner part of its orbit, the Moon must now slow back down to its original speed allowing the Earth to pass by. Lastly, as The Moon passes behind the Earth’s orbital path around The Sun, it must once again quickly accelerate back up to nearly 68,888 miles per hour before getting left in the dust by the Earth.
The Same Principles Apply to The Sun and The Earth
In addition to all of this, The Sun, itself is allegedly orbiting The Milky Way Galaxy at 448,000 miles per hour while The Earth is allegedly orbiting The Sun at 66,600 mph, further compounding the problems and calculations of the Heliocentric Model. The same issues that are involved with The Moon passing though the elliptic in front of The Earth apply to The Sun and The Earth, etc.. all the way out into the extremities of The Solar System. The problem of a celestial body passing in front of another celestial body, which is racing at an insane orbital velocity, applies regardless of the scale we use.
The Earth Does Not Perceptibly or Significantly Change its Orbital Velocity Around The Sun According to NASA
In The Heliocentric Model, The Earth completes one revolution around the Sun while spinning on its axis at 1000 mph. On a year-to-year basis, Earth’s orbital changes are so minuscule that they’re practically imperceptible and are considered negligible by Astronomers who measure it. Hence, The Earth does no change its orbital velocity and does not experience the same speeding up and slowing down via a gravitational “whiplash effect” as is said to be attributed to The Moon in relationship to The Earth.
Now, if all these accelerations and decelerations were actually true, then the Earth, Moon, and other planets would all have yet another set of ridiculous and impossible corkscrewing accelerations and decelerations necessary just to keep up with the Sun. And for the cherry on top all of these calculations have been assuming perfectly circular orbits, but the actual Heliocentric Model claims that the Moon's orbit around the Earth, the Earth's orbit around the Sun, and the Sun's orbit around The Milky Way are all elliptical not circular, meaning there would be even more additional accelerations and decelerations to calculate, depending where each one is along its elliptical path.
These constant and drastic accelerations and decelerations necessitated by the Heliocentric model are rarely if ever mentioned by globe believers because they have always been taught that the reason we do not feel or experience any of this supposed motion is because we always travel at a constant velocity. However, in their own model, due to these various elliptical orbits and the notion that such bodies are revolving around other revolving bodies, the Moon, Sun, Earth, and other planets could not maintain constant velocities and would instead be regularly accelerating and decelerating. Yet meanwhile, you can stack a house of cards, make a rock tower, or play a game of Jenga all without any of this motion, acceleration, and deceleration ever being felt or experienced.
Pseudo-Scientific Moon Mathe-Magic--Eric Dubay:
Constant Acceleration Versus Constant Velocity
When an object moves with a constant velocity, it means that the moving object has no acceleration. However, when an object moves with constant acceleration, its velocity changes by a constant amount throughout the same time interval.
Velocity
Velocity is the physical term that gives information about the rate of change of an object or body’s displacement. Thus, if an object changes its displacement from Point A to Point B over a time interval, its velocity may be calculated. Thus, when the distance traveled in one direction is the same during each time interval, then the velocity of an object or body is said to be constant.
Acceleration
Acceleration is also the physical term that gives information about the rate of change of an object or body’s velocity. Thus, when a moving object is changing, its speed in one direction is the same during each time interval, then the acceleration of an object or body is said to be constant. Thus, if an object changes its velocity from Point A to Point B over a time interval, its acceleration a may be calculated, as well.
Constant Velocity Versus Constant Acceleration
When anything has constant acceleration, it means that its velocity change is the same in each time interval. It means it is subjected to the same amount of force throughout the motion. As a result, constant acceleration does not imply constant velocity at all.
Motion with constant velocity and constant acceleration has totally different meanings. Suppose any object or body is traveling with a constant velocity. It means that it continuously travels at the same speed and also in the same direction. If the velocity of an object or body is constant, then its velocity is not changing, and thus, it has no acceleration with time. Consider you are driving on the highway on one way where your speedometer indicates the same speed, then it is said that you are traveling with constant velocity.
Constant acceleration is quite different from constant velocity. Suppose any object or body is moving with constant acceleration. It means that the velocity of an object or body is changing, but the rate at which it is changing is always constant.
Now consider The Earth and The Moon’s orbital trajectories. They are both constantly changing direction in their alleged elliptical paths, which translates to noticeable motion by any person who is involved in this Heliocentric fantasy of orbital mechanics. And yet, we feel none of this motion because it is just that…a fantasy. In short, both The Earth and The Moon are under constant acceleration, not constant velocity in The Heliocentric Model of The Cosmos.
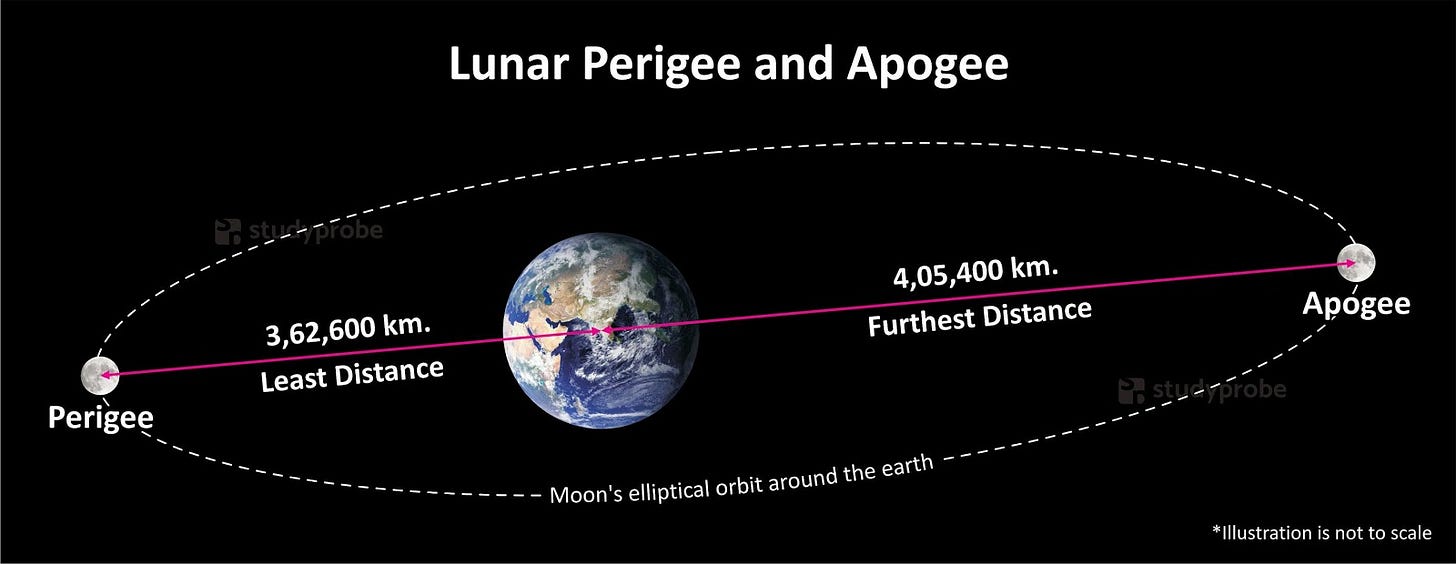
The Heliocentric Explanation For The Moon’s Motion
In The Heliocentric Model, The Moon revolves around Earth in an elliptical orbit with a mean eccentricity of 0.0549. Thus, the Moon's center-to-center distance from Earth varies with mean values of 363,396 km at perigee to 405,504 km at apogee. The point of the orbit closest to Earth is called perigee, while the point farthest from Earth is known as apogee.
The lunar orbital period with respect to the stars (sidereal month) is 27.32166 days (27d 07h 43m 12s). However, there are three other orbital periods or months that are crucial to the understanding and prediction of eclipses. These three cycles and the harmonics between them determine when, where, and how solar and lunar eclipses occur. The mutual gravitational force between the Sun and Moon is over twice as large as between the Moon and Earth. For this reason, the Sun plays a dominant role in perturbing the Moon's motion. The ever-changing distances and relative positions between the Sun, Moon, and Earth, the inclination of the Moon's orbit, the oblateness of Earth, and (to a lesser extent) the gravitational attraction of the other planets all act to throw the Moon's orbital parameters into a constant state of change. Although the Moon's position and velocity can be described by the classic Keplerian orbital elements, such “osculating elements” (i.e. a curve or surface touching another curve or surface so as to have a common tangent at the point of contact) are only valid for a single instant in time (Chapront-Touze' and Chapront, 1991). Nevertheless, these instantaneous parameters are of value in understanding the Moon's complex motions particularly with respect to the three major orbital cycles that govern eclipses.
The Moon's Orbit and Eclipses in The Heliocentric Model:
The Variability of the Moon’s Apparent Motion Through the Sky According to The Heliocentric Model
According to The Heliocentric Model, the average motion of the Moon in the sky is 13.2 degrees per day. This motion does vary, though, due to two effects. First, the orbit of the Moon is an ellipse whose center is offset by about 12,000 miles from the center of the Earth. As a result, during each orbit the distance to the Moon varies by twice this offset of 12,000 miles. During half its orbit it is approaching us, and during the other half it is moving away from us. During the half of the Moon’s orbit that it is approaching us, the mutual gravitational pull of the Earth-Moon system accelerates the Moon, causing it to move faster, until at the closest point in its orbit, called its orbital perigee, the Moon is moving about 6% faster than its average motion. Similarly, during the half of the Moon’s orbit that it is moving away from us, our mutual gravitational pull of the Earth-Moon system decelerates the Moon, causing it to move slower, until at the furthest point in the orbit, called its orbital apogee, the Moon is moving about 6% slower than its average motion.
In addition to these actual changes in velocity, there is an apparent change in the Moon’s motion caused by the fact that the Moon is closer or further from us. When it is closer to the Earth any motion that it has looks faster in angular terms than when it is farther away. This effect causes another 6% apparent increase or decrease in the apparent velocity of the Moon’s motion in the sky, in addition to the actual change.
If you sum these two effects, you find that as the Moon approaches perigee its angular speed among the stars will appear to increase by about 12% of its average speed, half of that change being due to its closer distance, and half being due to an actual increase in speed. Then, as the Moon approaches apogee, its angular speed among the stars will appear to decrease by about 12% of its average speed, with half of that change being due to its greater distance, and half being due to an actual decrease in speed. Since 12% of 13.2 degrees per day is 1.6 degrees per day, the daily motion of the Moon to the east can vary from as little as 11.6 degrees per day near apogee to as much as 14.8 degrees per day near perigee.
Does The Heliocentric Model Comport With the Necessary and Expected Lunar Acceleration and Deceleration Variances Required For a Functional Elliptical Orbit?
From the aforementioned, we know that if we are to apply The Heliocentric Model to The Moon’s elliptical orbit around The Earth, the Moon would then be traveling at 68,888 miles per hour when it reached the front of the Earth’s orbital path. At this point, since the Moon is allegedly 240 thousand miles away from the Earth, the Earth would catch up in just four hours, and so the Moon must continue traveling 66,600 miles per hour along Earth's trajectory while simultaneously continuing its now perpendicular 2,288 mile per hour second trajectory.
Then as it turns to reach the inner part of its orbit, the Moon must now slow back down to its original speed allowing the Earth to pass by. Lastly, as The Moon passes behind the Earth’s orbital path around The Sun, it must once again quickly accelerate back up to nearly 68,888 miles per hour before getting left in the dust by the Earth. In addition to all of this, the Sun, itself, is allegedly orbiting The Milky Way Galaxy at 448,000 miles per hour, further compounding the problems and calculations of the Heliocentric Model.
Now Add The Elliptical Orbit Gravitational Whiplash Effect
It says that during the half of the Moon’s orbit that it is approaching us, the mutual gravitational pull of the Earth-Moon system accelerates the Moon, causing it to move faster, until at the closest point in its orbit, called its orbital perigee, the Moon is moving about 6% faster than its average motion in an elliptical orbit. That 6% increase in orbital velocity is said to occur from a kind of gravitational whiplash effect.
As the story goes, this dynamic elliptical behavior is due to the gravitational pull of the Sun on the Moon as it orbits Earth. Consequently, a continuous torque is applied to the lunar orbit in an unsuccessful effort to permanently align the major axis towards the Sun. The annual orbit of the Earth-Moon system around the Sun coupled with the Moon's synodic orbit around Earth mean that the conditions for such a permanent alignment are always changing. The overall effect is to twist and distort the shape and orientation of the Moon's elliptical orbit.
Ok, so that is 6% of The Moon’s average velocity, which is 2,288 mph times .06, which equals approximately plus or minus 137 mph in variance. And so, as The Moon races to catch up with The Earth in its elliptical orbit, that comes to 2,288 mph plus 137 mph, which equals 2,425 mph. But we must remember that The Earth is still traveling at 66,600 mph while The Moon is executing this acceleration. Adding 66,600 mph to 2,425 mph we get 69,025 mph.
And so, without the gravitational whip effect, we have 68,888 mph, and with it, we have 69,025 mph. That’s pretty close. Hence, the gravitational whip effect becomes the explanation for how The Moon can hold its elliptical orbit around The Earth as The Earth travels at 66,600 mph in its elliptical orbit around The Sun.
Nevertheless, there is still one component that continually undermines the Heliocentric explanation:
The Moon is passing infront of The Earth as The Earth travels at 66,600 mph in its elliptical orbit around The Sun, and since it does not speed up significantly enough to avoid The Earth crashing into it in The Earth’s forward elliptical orbit around The Sun (only a 6% velocity increase, which is merely an extra 137 mph), then we must accept that The Earth’s gravitational pull magically reverses polarity to become a repulsive force instead of an attractive force, and thereby, somehow pushes The Moon away from it as The Moon passes in front of The Earth as The Earth travels at 66,600 mph in its elliptical orbit around The Sun.
This problem will always be a thorn in The Heliocentric side as it does not comport with logic and reason to assume that The Moon is being both attracted in some instances by Gravity and repelled in others by this magical idea of Gravity. It is one thing to assert that The Earth is pulling The Moon like a tractor beam through The Solar System, but it is quite another thing to assert that The Earth is suddenly pushing The Moon away and keeping it a distance as The Earth advances at 66,600 mph towards it in its elliptical orbit around The Sun. This paradox of Gravity acting act both an attractive force, and then suddenly a repulsive force when its suits the narrative of The Heliocentric Model, is the elephant in the room that Heliocentrists will cover up, again and again, with regards to The Moon’s alleged ability to remain in orbit with a rock that is allegedly travelling at 66,600 mph around The Sun, by inserting yet another impossible claim.
And that claim is:
…the idea that The Earth’s gravitational pull is not exclusively necessary in order to keep The Moon in its delicate forward motion, and in orbital equilibrium around The Earth, as The Earth travels at 66,600 mph in its elliptical orbit around The Sun.
The Moon Cannot Be Said to be in Constant Forward Motion in its Orbital Path Around The Sun as it Orbits Conjoined Around The Earth
Heliocentrists have this misconception that The Moon is in some kind of forward momentum as it orbits The Sun along with The Earth. And with this misconception deeply embedded in their delusional minds, they attempt to assert that The Moon is keeping up with The Earth as The Earth travels at 66,600 mph in its elliptical orbit around The Sun. The idea behind this delusion is to claim that The Earth’s gravitational pull is not exclusively necessary in order to keep The Moon in its delicate orbital equilibrium around The Earth as The Earth travels at 66,600 mph in its elliptical orbit around The Sun. However, there is one little detail that they fail to entertain, and that is the fact that in The Heliocentric Model, The Moon is in orbit around The Earth, which means it must travel in the opposite direction of The Earth at specific times as it orbits around it, and when something is traveling in the opposite direction it can no longer be said have forward orbital momentum around The Sun.
In fact, as The Moon orbits around The Earth, The Earth is supposed to be travelling at 66,600 mph in the opposite direction of The Moon in its elliptical orbit around The Sun. And so, the only thing left is the claim of magic Gravity to hold The Moon stuck to an Earth in a delicate orbital equilibrium while The Earth is allegedly travelling at 66,600 mph in the opposite direction of The Moon in its elliptical orbit around The Sun. And with that claim, as has already been established, we are back to a another set of ridiculous and impossible corkscrewing accelerations and decelerations necessary just to keep up with The Sun. And yet, we observe none of this, and the days, months, and years do not reflect such Helter Skelter motion in The Moon.
Additionally, when Ther Moon, traveling at 2,288 mph, emerges from its perigee, and begins to transcribe its elliptical orbit perpendicular to The Earth’s forward 66,6000 mph trajectory, it finally passes in front of The Earth, which constitutes lateral movement across the elliptic (the ecliptic or ecliptic plane is the orbital plane of Earth around the Sun), and can no longer be said to be in forward motion with The Earth. In Astronomy and Physics, with respect to relative reference frames, you cannot go forward while in an elliptical orbit while simultaneously going laterally. These are two different vector reference frames. You would need to detach from the elliptical orbit in order to achieve such a parabolic arc forward while also moving laterally.
This being the case, as The Moon travels at 2,288 mph and slogs past The Earth, which is hurling forward in its elliptical orbit at a mind-bending 66,6000 mph, it would enter into lateral motion, perpendicular to The Earth’s forward orbital trajectory, and get left in the dust in seconds. And if the claim is made that The Earth holds The Moon in front of it as it speeds along by some magical reconfiguring of Gravity as a reverse polarity mechanism, thereby suddenly becoming a repulsive force instead of an attractive force, then The Earth, with a forward motion of 66,6000 mph, would most certainly crash into The Moon, as The Earth is four times as large as The Moon in The Heliocentric Model. Again, as soon as The Moon changes direction in its orbit, imaginary Gravity has no say in the matter, in that Gravity is supposed to be an attractive force. But as The Moon emerges from its perigee, relative to The Earth, and is front of the ecliptic, its orbital integrity requires that The Earth’s Gravity repel or push The Moon forward, at that point. The blatant contraction in this absurdly illogical situation reveals the fallacious nature of The Heliocentric Model, as well as its science fiction underpinnings.
What Does it Mean to Emerge From Perigee and Go “Beyond The Ecliptic”?
What is The Ecliptic Plane?
In The Heliocentric Model, the ecliptic, or ecliptic plane, is the orbital plane of Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the background of stars. The ecliptic is an important reference plane in The Heliocentric Model and is the basis of the ecliptic coordinate system Obliquity of the ecliptic.
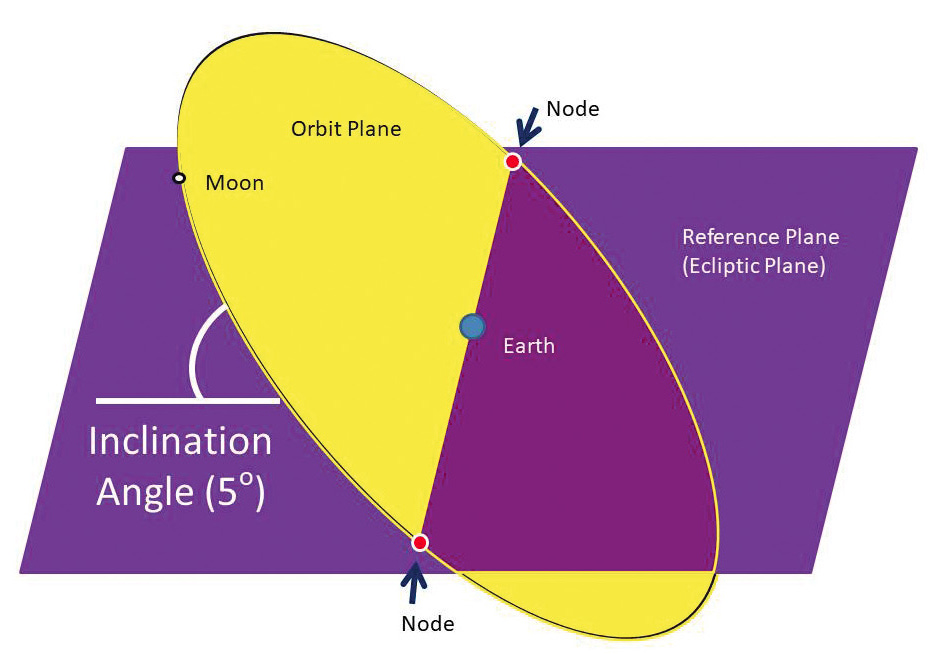
Orbital Inclination: The Moon's orbit is inclined by 5.14° to the ecliptic. This shows the specific configuration at major northern lunistice. At such times, the earth's north pole is toward the moon and the moon is north of the ecliptic:
Tilt or Obliquity of The Ecliptic
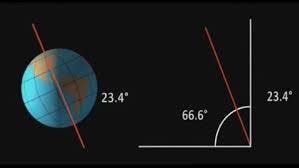
Obliquity of the ecliptic is the term used by astronomers for the inclination of Earth's equator with respect to the ecliptic, or of Earth's rotation axis to a perpendicular to the ecliptic. It is about 23.4° 9 (or 66.6 degrees…there’s that number again) and is currently decreasing 0.013 degrees (47 arcseconds) per hundred years because of planetary perturbations. Finally, the Moon does not orbit around the Earth directly above our equator. The Moon's orbit is tilted by 6.7 degrees to the Earth's equator.
The Moon and The Ecliptic
In The Heliocentric Model, The Moon isn’t exactly on the ecliptic. Its orbit around Earth is tilted by about 5.15 degrees relative to the ecliptic. This means The Moon spends most of its time above or below the ecliptic. It crosses it twice each orbit, once going upward and once downward relative to our point of view. Therefore, we usually see the Moon close to, but not exactly alongside, the other solar system objects.
And so to go “beyond the ecliptic” is to emerge from perigee and rise above or dip below the ecliptic. When the Moon is closest to the Earth (perigee), it moves faster, while when it is furthest from the Earth (apogee), it moves slower. Perigee is when The Moon experiences the “gravitational whipping” effect that Heliocentrists are so fascinated by. The Moon's orbit around Earth is elliptical. The point of the orbit closest to Earth is called perigee, while the point farthest from Earth is known as apogee.
Kepler's Laws of Planetary Motion
In astronomy, Kepler's Laws of Planetary Motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun, and variations of them apply to The Moon’s elliptical orbit around The Earth.. The laws modified the Heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary.
The Three Laws State That:
1. The orbit of a planet is an ellipse with the Sun at one of the two foci.
2. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
3. The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The third law expresses that the farther a planet is from the Sun, the slower its orbital speed, and vice versa.
Isaac Newton showed in 1687 that relationships like Kepler's would apply in the Solar System as a consequence of his own Laws of Motion And Law of Universal Gravitation.
Kepler's First Law says that planets have elliptical orbits. As a result, the distance between a planet and the Sun changes rhythmically as the planet moves in its orbit. In many cases, this rhythmic change is rather subtle; for example, the Earth's distance from the Sun varies between 98.3% and 101.7% of its average value. (By the way, the Sun is closest in January, and furthest in July, so this change doesn't explain the seasons!) In contrast, the ellipticity of the Moon's orbit is fairly dramatic; the Moon's distance from the Earth varies between 92.7% and 105.8% of its average value of 384,400 km.
This variation in distance produces several effects which we can observe here on Earth. For example, when the Moon is closest to the Earth (perigee), it moves faster, while when it is furthest from the Earth (apogee), it moves slower. The Moon also appears to nod back and forth a bit as it orbits the Earth. But the most dramatic effect is the change in the Moon's apparent diameter: when the Moon is close, it looks larger, and when the Moon is far, it looks smaller. We will use this effect to study the change in the Moon's distance.
The Moon, The Earth, and Kepler’s Second Law
Kepler’s Second Law of Planetary Motion, in astronomy and classical physics, one of three laws describing the motions of the planets in the solar system and which states that a radius vector joining any planet to the Sun sweeps out equal areas in equal lengths of time.
The validity of Kepler’s second law means a planet must have a higher-than-average velocity near perihelion (when it is closest to the Sun) and a lower-than-average velocity near aphelion (when it is farthest away from the Sun). The angular velocity must vary around the orbit in a similar way.
The variance in the Moon's orbital distance corresponds with changes in its tangential and angular speeds, as stated in Kepler's Second Law. of Moon's elliptical orbit rotates by one complete revolution once every 8.85 years in the same direction as the Moon's rotation itself.
In a Nutshell
In a Nutshell, there are only two options as soon as The Moon, traveling at 2,288 mph, emerges from its perigee, and begins to transcribe its elliptical orbit perpendicular to The Earth’s forward 66,6000 mph trajectory, beyond the ecliptic:
1. As The Moon travels at 2,288 mph, entering into lateral motion, perpendicular to The Earth’s forward orbital trajectory, which is hurling forward in its elliptical orbit at a mind-bending 66,6000 mph, The Moon gets left in the dust in seconds.
2. The Earth crashes into The Moon as The Moon saunters along at 2,288 mph infront of a 66,600 mph Earth, which is four times The Moon’s size.
In other words, as soon as The Moon passes beyond the elliptic (the ecliptic or ecliptic plane is the orbital plane of Earth around the Sun), it can no longer be said to be in forward motion with The Earth. Objects moving laterally are no longer moving forward. In Astronomy and Physics, with respect to relative reference frames, you cannot go forward while in an elliptical orbit while simultaneously going laterally. These are two different vector reference frames. You would need to detach from the elliptical orbit in order to achieve such a parabolic arc forward while also moving laterally.
As soon as The Moon emerges from its perigee, relative to The Earth, and is front of the ecliptic, its orbital integrity requires that The Earth’s Gravity repel or push The Moon forward, at that point. However, Gravity is an attractive force, not a repulsive force, and so The Earth’s “gravitational well” provides no mechanism to hold The Earth as soon as The Moon emerges from its perigee beyond the ecliptic. The blatant contraction in this absurdly illogical situation reveals the fallacious nature of The Heliocentric Model, as well as its science fiction underpinnings.
Only in a static model could The Moon orbit around The Earth with any chance of preserving its elliptical orbit.
Additionally, you simply cannot have it both ways for these reasons:
1. A hyper-powerful Gravitational force that holds The Moon in a delicate elliptical orbit while The Earth bullets at a mind-bending 66,600 mph in its elliptical orbit around The Sun.
2. And also an enervated and feeble Gravitational force that allows trillions of tons of clouds to remain aloft effortlessly.
However you slice, it The Heliocentric Model emerges as a wild and spurious science fiction explanation of orbital mechanics if we take it seriously…and that’s why we can’t.
Where Does The Whiplash Gravitational Effect Occur in The Moon’s Elliptical Orbit?
Another thing to keep in mind is that in order for The Moon to whip around The Earth when it is front of it, and not get hit by a speeding Earth at 66,600 mph, it would need to whip around infront of it, and not at any other point along its elliptical path. This is so because the maximum velocity required to get out of the way of a speeding Earth is required directly in The Earth’s path, and not anywhere else. But this is not the case. In fact the gravitational whiplash region is rarely lined up infront of The Earth at perigee, (the point of the orbit closest to Earth), thereby disproving The Heliocentric explanation as a viable model to explain how The Earth never crashes into The Moon as The Moon saunters along at 2,288 mph infront of a 66,600 mph Earth.
The Freefall of The Moon in a Dynamic Model Versus a Static Model
In Newtonian physics, Free Fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on it.
An object in the technical sense of the term "free fall" may not necessarily be falling down in the usual sense of the term. An object moving upwards might not normally be considered to be falling, but if it is subject to only the force of gravity, it is said to be in free fall. The Moon is thus in free fall around the Earth, though its orbital speed keeps it in very far orbit from the Earth's surface.
In a roughly uniform gravitational field gravity acts on each part of a body approximately equally. When there are no other forces, such as the normal force exerted between a body (e.g. an astronaut in orbit) and its surrounding objects, it will result in the sensation of weightlessness, a condition that also occurs when the gravitational field is weak (such as when far away from any source of gravity).
The term "free fall" is often used more loosely than in the strict sense defined above. Thus, falling through an atmosphere without a deployed parachute, or lifting device, is also often referred to as free fall. The aerodynamic drag forces in such situations prevent them from producing full weightlessness, and thus a skydiver's "free fall" after reaching terminal velocity produces the sensation of the body's weight being supported on a cushion of air.
Now, if the Earth existed in a static model and did not move, then a case could be made that The Moon is in freefall around it, while also orbiting, such that it would not crash into the Earth. But that scenario implies a static model, where The Earth is stationary. However, The Heliocentric Model is dynamic model, where The Earth is moving in an elliptical orbital trajectory at 66,6000 mph. Because The Heliocentric Model involves the Earth traveling at 66,600 mph, this means the freefall hypothesis does not apply. In other words, we still must contend with the fact that The Earth should crash into The Moon as The Moon saunters along at a leisurely lateral path of 2,288 mph, perpendicular to The Earth, and in front of The Earth’s speeding 66,600 mph trajectory. Nevertheless, The Earth does not crash into The Moon because The Heliocentric Model is fictitious, and is not based upon accurate measurements, observations, or empirical data.
An accurate model from NASA of how the “planets” orbit the Sun in The Heliocentric Model, which then moves through the galaxy in a different direction-of-motion. Note that the planets are all in the same plane and are not dragging behind the Sun or forming a wake of any type. The planets change position relative to one another, making them change their apparent positions.
Do you see the impossibility of this model being realized in the real world?
Gregory Lessing Garrett’s Newsletter is a reader-supported publication. To receive new posts and support my work, consider becoming a free or paid subscriber.