Issues With Lunar Laser Ranging Experiment: The Retroreflectors on The Moon Hoax
Alleged Laser Ranging Retroreflector on The Moon…Hahaha!
Lunar Laser Ranging (LLR) is the practice of measuring the distance between the surfaces of the Earth and the Moon using laser ranging. Allegedly, the distance can be calculated from the round-trip time of laser light pulses travelling at the speed of light, which are reflected back to Earth by the Moon's surface or by one of five retroreflectors installed on the Moon during the Apollo program (11, 14, and 15) and Lunokhod 1 and 2 missions.
Aiming a laser at The Moon 294,000 miles away, through seven layers of Earth atmosphere, while the Earth is spinning at 1000 mph, and orbiting The Sun at 67,000 mph, while The Milky Way Galaxy shoots out at 831,000 kph, and while the entire Milky Way Galaxy is also allegedly hurling for decades and millions of mph on the membrane of an expanding Universe, at a spot on The Moon the size of a book, which has been covered by dust and debris for decades, and contorted by millions of thermal cycles, and having that book size retroreflector magically refocus and reflect the ray back to Earth, at the same location it was sent on a moving spinning Earth, under the same aforementioned conditions as it left Earth………….is Ludicrous!
Allegedly, when astronauts visited the Moon more than 50 years ago, they left a series of retroreflecting mirrors on the lunar surface. When scientists here on Earth shoot a laser at the Moon, the light from the laser is reflected right back at them from one of these devices. For every 100 quadrillion photons shot at the Moon, only a handful come back, but that’s allegedly enough to get an accurate appraisal.
Well, at least the official story, but looks at the science behind all this.
Shooting Lasers at the Moon - Real or Memorex?
To The Moon and Back in a Vacuum…The Scientism Explanation:
If this laser test was shot in a vacuum, it would take approximately 2.5 seconds for the laser beam to travel to The Moon and back to The Earth. Since light is moving at almost 300,000 kilometers (186,411 miles per second), it takes a little more than a second to make the journey. And then it takes another second or so to return. By calculating the exact amount of time it takes for light to make the journey, astronomers are able to know exactly how far the Moon is at any time, down to millimeter accuracy.
Ok, what is wrong with this story?
This 2.5 second only exits if there is vacuum between The Moon and The Earth, But there is not. There is atmospheric distortion caused by seven atmospheric layers, debris, pollution, electromagnetic fields, and atmospheric vapor to contend with, causing refraction and severe beam divergence.
The distance to the Moon is calculated approximately using the equation: distance = (speed of light × duration of delay due to reflection) / 2. Since the speed of light is a defined constant, conversion between distance and time of flight can be made without ambiguity.
The Basics of Lunar Ranging
The basic idea is that we want to test our understanding of gravity to unprecedented precision. The earth-Moon system is an ideal laboratory for performing such a measurement. The earth and Moon are attracted to each other and to the sun by gravity, so that studying the dynamics of this system is a way to explore the precise behavior of gravity. For instance, we can ask the question: "do the earth and Moon fall toward the sun with the same acceleration?" To do this, we need to measure the exact shape of the lunar orbit. We want to measure the earth-Moon distance at various points in the lunar cycle (crescent, quarter Moon, gibbous, and full phases). Each measurement will be precise to one millimeter—about the thickness of a paperclip. We do this by measuring the round-trip travel time of a light pulse bouncing off lunar reflectors. Multiplying this time by the speed of light gives us the distance. In addition to characterizing the shape of the lunar orbit, we will be able to follow the slow recession of the lunar orbit by 3.8 cm (1.5 inches) per year due to tidal friction.
One way to state why millimeter-precision measurements help us understand gravity is: any theory of gravity will predict certain specific paths/orbits of the bodies under its influence, given initial conditions. Is general relativity predicting exactly the correct path for the Moon? If not, we've got trouble. General relativity (GR) predicts deviations from Newtonian gravity at the several-meter level in the lunar orbit. So millimeter-level measurement precision puts GR to a hard test.
What's the point?
When Einstein came up with his theory of general relativity, he claimed that this was a better description of gravity than Newton's time-tested and very successful model. Many reacted with healthy skepticism—nobody was complaining about deficiencies in Newtonian gravity (at least not many people were). But today, test after test has shown that Newtonian gravity doesn't cut it in ultra-precise tests. It's still good enough to plan interplanetary probe trajectories, but not good enough to describe everything we see. And surprisingly, understanding general relativity is absolutely vital in getting the global positioning system (GPS) to work. This system would utterly fail in an hour's time if we didn't anticipate that time runs more slowly in a gravitational field—a consequence predicted by general relativity.
Today, there is a growing sentiment in the physics and astrophysics communities that general relativity is likely not the last word on gravity. First, GR is not compatible with quantum mechanics. Maybe we live in the kind of universe where we can have two incompatible descriptions of the fundamental rules of how matter behaves and interacts. But past reductions/unifications (e.g., electricity and magnetism; the weak nuclear force and electromagnetism) suggest otherwise. Who would you bet on? Aspects of quantum mechanics have been tested to phenomenal precisions: part-in-a-trillion levels. But GR has been tested only to part-in-100,000 levels so far. It's more likely to be incomplete than is quantum mechanics. And perhaps more convincingly, we now see that the expansion of the universe is accelerating! This is a total surprise, and not consistent with the predictions of general relativity. It is highly likely that the solution to this puzzle will involve a modification to or replacement of general relativity.
Lunar laser ranging has been performed for the past 35 years, now reaching a precision of 2 centimeters. APOLLO (the Apache Point Observatory Lunar Laser-ranging Operation) will improve this performance by at least a factor of ten. While this factor of ten (or better) may not be enough to expose a shortcoming in the theory of general relativity, there is a chance that it will. We can't afford not to look. At the very least, APOLLO will place more stringent constraints on existing and future alternatives to Einstein's theory of gravity. Many new phenomena are discovered in science by looking closely at things we think we understand perfectly, only to find that our knowledge or understanding is incomplete.
Ultra-Short Bursts of Light:
How do we measure the distance to the Moon to such phenomenal precision? We "ping" the Moon with ultra-short pulses of light. To do this, we have a laser that generates intense bursts of light only 100 picoseconds long—that's one tenth of a billionth of a second! Light, which travels 7 earth circumferences every second, only travels about an inch in this time. So these pulses are like little "bullets" of light.
Better than a stopwatch...
In essence, we measure the time it takes for the pulse of light to travel to the Moon and back. This can take anywhere from 2.34 to 2.71 seconds, depending on how far away the Moon is at the time (the earth-Moon distance ranges from 351,000 km to 406,000 km). We can time the round trip to few-picosecond precision, or a few trillionths of a second.
But what do we measure to?
We measure to the retroreflector arrays left on the Moon by the Apollo astronauts, and by an unmanned Soviet rover carrying a French-built reflector. These define very specific points of reference on the lunar surface. This is far better than measuring to the rough-and-tumble surface. We would never have any hope of measuring the lunar distance to millimeter precision without these well-defined reflectors. We aim at one reflector at a time when performing the measurement.
Where on Earth do we measure from?
The telescope used for APOLLO has a 3.5-meter diameter mirror and is located at the Apache Point Observatory in southern New Mexico. We use the telescope as a gigantic (3.5 meter wide) laser pointer and also as a signal receiver. We reference our measurements to the center of the telescope mount, where the azimuth axis and elevation axis intersect each other. As the telescope swings around to point at different parts of the sky, this point stays fixed—almost.... The position of the telescope relative to the center of the earth isn't as stationary as you might imagine. The continental plate drifts, the tides from the Moon and sun make the site swell by about a foot twice a day, weather systems can push the local crust down, etc. We have to be aware of all of these influences and take them into account in order to extract the scientifically useful center-to-center distance between the earth and Moon.
The observing technique:
We will typically measure the distance to each of the four available reflectors in turn over a half-hour period. Then we'll do the same thing a few nights later. By doing this over months and years, we will characterize the shape of the lunar orbit to high enough precision to be able to say something about the workings of Gravity.
The pointing challenge:
To concentrate as much laser power as possible onto the reflector array, we must ensure that the beam leaving the telescope is as collimated (parallel, non-diverging) as possible. We use a laser both because we can get ultra-short pulses of light from a laser, and also because the light from a laser is extraordinarily directional—not diverging the way a flashlight, or even searchlight, would. Even so, the turbulent atmosphere distorts the beam, imparting a divergence of about one arcsecond (sometimes more). One arcsecond is 1/3600th of a degree, or the angular size of a quarter about five kilometers (about 3 miles) away. At the distance of the Moon, this angle translates to 1.8 kilometers (just over a mile). Though this is large compared to the size of the reflector (most of the light is wasted—never hitting the reflector), it is still a challenge to point and maintain the laser beam on this tiny patch of the Moon.
-- https://tmurphy.physics.ucsd.edu/apollo/basics.html
Problematic Factors Included in The Heliocentric Scientism Model:
1. The location of the Moon in the sky
2. The relative motion of Earth and the Moon
3. Earth’s rotation
4. Van Allen belt radiation perturbations
5. Lunar libration
6. Laser beam Diffusion of Distance
7. Polar motion
8. Weather
9. The Inverse Square Law of Light
10. Speed of light in various parts of the atmosphere
11. Propagation delay through Earth’s seven layers of atmosphere
12. The location of the observing station and its motion due to crustal motion and tides
13. Relativistic effects
Data Analysis
The Lunar Laser Ranging data is collected in order to extract numerical values for a number of parameters. Analyzing the range data involves dynamics, terrestrial geophysics, and lunar geophysics. The modeling problem involves two aspects: an accurate computation of the lunar orbit and lunar orientation, and an accurate model for the time of flight from an observing station to a retroreflector and back to the station. Modern Lunar Laser Ranging data can be fit with a 1 cm weighted rms residual.
The center of Earth to center of Moon distance is computed by a computer program that numerically integrates the lunar and planetary orbits accounting for the gravitational attraction of the Sun, planets, and a selection of asteroids. The same program integrates the 3-axis orientation of the Moon called physical Libration.
Problematic Factors Included in The Laser Range Model
1. The position of the ranging station accounting for motion due to plate tectonics, Earth rotation, precession, nutation, and polar motion.
2. Tides in the solid Earth and seasonal motion of the solid Earth with respect to its center of mass.
3. Relativistic transformation of time and space coordinates from a frame moving with the station to a frame fixed with respect to the solar system center of mass. Lorentz contraction of the Earth is part of this transformation.
4. Delay in the Earth’s atmosphere.
5. Relativistic delay due to the gravity fields of the Sun, Earth, and Moon.
6. The position of the retroreflector accounting for orientation of the Moon and solid-body tides.
7. Lorentz contraction of the Moon.
8. Thermal expansion and contraction of the retroreflector mounts.
9. For the terrestrial model, the IERS Conventions (2010) is a source of detailed information.
Due to Thermal Cycles and Dust, a Retroreflector on The Moon Would Be Completely Non-Reflective and Contorted By Now
Not only would the alleged retroreflector on The Moon be completely covered in dust by now, but its surface would be contorted beyond recognition by millions of thermal cycles as The Moon’s surface experiences thermal fluctuations from hotter to colder, day after day, week after week, month after month, and year after year.
Home roofing experiences thermal cycles even with relatively small variances in temperature, when compared to The Moon’s surface, and they are tattered and atrophied from even this small variance.
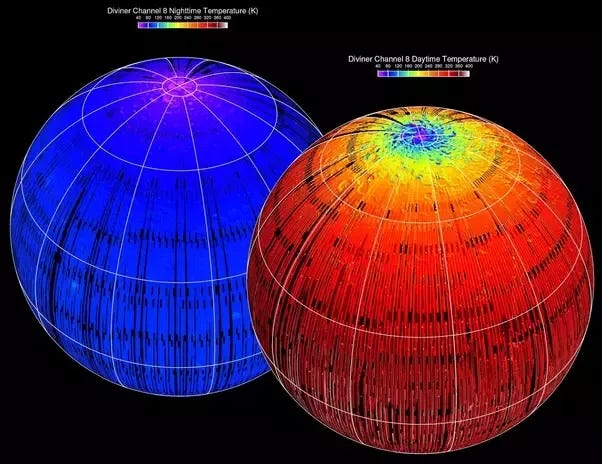
Taking the Moon's Temperature:
Daytime temperatures near the lunar equator reach a boiling 250 degrees Fahrenheit (120° C, 400 K), while nighttime temperatures get to a chilly -208 degrees Fahrenheit (-130° C, 140 K). A thermal cycle is defined as any recursive thermal test in which the temperature is regularly altered, touching a high-temperature peak and a low-temperature peak. Hence, a retroreflector on The Moon would be completely non-reflective and contorted by now.
The Effect of Thermal Fatigue on Metal and Retroreflectors:
Also, the distance continually changes for a number of reasons, but averages 385,000.6 km (239,228.3 mi) between the center of the Earth and the center of the Moon. The orbits of the Moon and planets are integrated numerically along with the orientation of the Moon called physical Libration.
Laser Light Diffuses Over Great Distances
Shooting a laser over 297,000 miles? What episode of Star Trek is NASA mimicking, now? Afterall, though laser light may start as a pinprick of concentrated light from Earth, it will diffuse over distance and become a wash of nebulous wash even after a few hundred miles, let alone, 297,000 miles. Hence, if laser light was reaching the Moon, it makes far more scientific sense that The Moon be about 3000 miles away instead of the Star Trek fictional 294,000 miles away.
How Far Can a Laser Shoot?
Laser beams get wider with distance. As the beam power becomes spread over a larger and larger area, the amount of light entering a pupil decreases. Even if the person is standing in a pitch-black part of the Earth at night, say in the middle of a vast desert, the eye is capable of reliably seeing a 6th magnitude star which is about 20 picowatts per square meter. A 5-milliwatt laser pointer, assuming it spreads at the usual 3 milliradians divergence angle, makes a spot at the Moon over 1000 kilometers in diameter. That results in a 3 femtowatt per square meter intensity. That is only about 0.015% of the intensity needed to travel back to The Earth. And then The Earth’s seven atmospheric layers would wash the remaining beam away, completely.
Beam Divergence Issues With Lunar Laser Ranging Experiment: Retroreflectors on The Moon
In electromagnetics, especially in optics, beam divergence is an angular measure of the increase in beam diameter or radius with distance from the optical aperture or antenna aperture from which the beam emerges. The term is relevant only in the "far field", away from any focus of the beam. Because of beam divergence, laser intensity can only be conserved at a limited distance.
Even the strongest lasers in the world experience beam divergence even after 10 miles. After 50 miles, the strongest laser in the world would still experience a beam divergence of anywhere from 8 to 14 feet, depending upon the atmospheric density and dust at the time. Now imagine a laser going 294,000 miles through 7 atmospheric layers and environment dust! There would be no pinpoint concentration left in the laser after 200 miles, and after 294,000 miles, the beam would be merely a washed-out fuzzy blur that spreads out over hundreds of miles, and certainly nothing concentrated enough for a dust covered, thermal cycle contorted retroflector to even detect, let alone, magically refocus the divergent wash of laser light back to Earth another 294,000 miles, and again through 7 layers of Earth atmosphere, all while the Earth is spinning at 1000 mph, while orbiting The Sun at 66,600 mph, and while The Moon orbits around The Earth at 2,300 mph.
Can a Laser Pointer Reach The Moon?
Well, it’s an imaginary yes and a realistic no.
Theoretically, a laser beam can reach the surface of The Moon, but the light would be too dispersed for any of us to see it. Even the strongest laser on Earth, known as The Confinement Beam, which releases a whopping 500 TW (terawatts) of power, doesn’t emit a laser strong enough to get to The Moon.
FUN FACT: Because the Confinement Beam is so powerful, researchers only fire it for a nanosecond for each use to avoid using up too much energy and resources on Earth.
How Much Power Would a Laser Pointer Need To Reach The Moon?
According to experiments, you’d need around 0.004 YW (yottawatts) to power a laser that’s strong enough to reach the surface of The Moon. This is one million billion, billion watts of power. That’s more than the available energy we have here on Earth. A watt is used to measure the flow of energy that is used, released or converted from one form to another. A kilowatt is 1,000 watts. Most home energy use is described as the number of kilowatts steadily used over an hour. But a yottawatt? That’s the measure scientists use for the energy released when imaginary black holes go crashing into each other. We having noting on Earth that can generate that kind of wattage.
To give you a clearer image of what that would look like:
To reach 0.004 YW, you’d have to give 8 million people their very own Confinement Chamber and simultaneously aim it at The Moon.
Laser Beam Divergence and Spot Size - Amrita University:
One only needs three rather simple equations to assess how far a laser can shoot.
First, if we assume the laser is optimized so that its spreading angle is at its theoretical minimum, then we can calculate its beam divergence (in radians) using this equation:
(The laser's wavelength)/(π × The laser's aperture)
Then a little bit of geometry will give us the size of the final lit spot at the destination:
π × (Beam divergence in radians × Distance)2
Finally, the brightness at the destination is given by dividing the output power of the laser over the area of the spot:
(The laser's power) / (Size of the spot)
Thus, by the time the laser light reaches the Moon, the glint would be a million times dimmer than the faintest light visible to the human eye. Then the far more absurd notion that this insanely diminished intensity laser light would travel back to The Earth after bouncing off of the highly inferior surface of a one-foot-wide Retroreflector on The Moon, culminating in a whopping 588,000 thousand miles round trip, is so comically ludicrous as to be beyond reasonable consideration.
How Far Can Laser Light Travel?
Have you ever played with a pocket-sized laser, wondering how far its light would travel? Could you, a naughty student inside a classroom on Earth, annoy a poor substitute teacher on Mars by waggling your laser pointer at him?
The dimmest light visible to the naked eye in perfect darkness is around one ten-billionth of a watt per square meter. However, with the presence of urban light pollution, one usually can’t see stars much dimmer than the North Star, which has an intensity of around four-billionths of a watt per square meter. For comparison, the full moon is almost a million times brighter at one-thousandth of a watt per square meter. Finally, the midday sun is at a whopping 1,000 watts per square meter, about half a million times brighter than The Moon.
In this article, we will be using these numbers as references.
The short answer: no.
By the time the light finally reached Mars, the glint would be a million times dimmer than the faintest light visible to the human eye.
But you don’t need to take our word for it. The math needed to calculate the answer is surprisingly simple. Partly inspired by a talk at a recent astronomy meeting that explored whether we could detect photons from potential exoplanet-dwelling aliens, Inside Science performed some of our own calculations to see if a hypothetical alien Galileo could observe photons coming from Earth.
All we need is an equation for calculating how quickly a laser beam spreads out as it travels through space. From that we can use straightforward geometry to derive the diameter of the beam when it hits its target. Finally, we divide the power output of the laser by the area of the final lit spot and voila! -- that's how intense the laser is at the destination. While the way humans, or aliens, perceive the brightness of this light is much less straightforward, for the purpose of this exercise we treat brightness and light intensity as the same thing.
The Math:
One only needs three rather simple equations for all the calculations done in this article.
First, if we assume the laser is optimized so that its spreading angle is at its theoretical minimum, then we can calculate its beam divergence (in radians) using this equation:
(The laser's wavelength)/(π × The laser's aperture)
Then a little bit of geometry will give us the size of the final lit spot at the destination:
π × (Beam divergence in radians × Distance)2
Finally, the brightness at the destination is given by dividing the output power of the laser over the area of the spot:
(The laser's power)/(Size of the spot)
If you didn’t make a mistake in your calculations and kept everything in radians, watts and meters, the final number should be in watts per square meter.
Your Pocket Laser Pointer:
The power for an average laser pointer is a measly 0.005 watts. However, because of the narrow path of the laser beam, if you pointed it directly at your eye from an arm's length away, the little illuminated dot on your eyeball would be 30 times brighter than the midday sun. So, don't do this at home, or anywhere.
Still, the narrow beam will spread out over long distances. Around 100 meters away from a red laser pointer, its beam is about 100 times wider and looks as bright as a 100-watt light bulb from 3 feet away. Viewed from an airplane 40,000 feet in the air -- assuming there’s no clouds or smog -- the pointer would be as bright as a quarter moon. From the International Space Station, it would fade to roughly as bright as the brightest star in the night sky -- Sirius.
For Starman, the dummy driving the Tesla car that Elon Musk's company Space X recently launched into space, your little red laser pointer would be too dim to notice. If you want to get his attention, you'll need something brighter.
The Navy's Missile-Killer:
The U.S. Navy might have what we need. According to recent reports, their current goal is to develop a laser that is both logistically practical and powerful enough to destroy incoming cruise missiles. A laser like that would need to put out about 500,000 watts of power -- 100 million times more powerful than your pocket laser pointer. These lasers typically operate in the infrared spectrum, which is invisible to humans. But for the sake of this exercise we'll assume that both Starman and the Martians can see in the infrared.
More Light and Laser Insight from Inside Science:
Weapons-grade lasers also tend to have a much larger opening, or aperture, which counterintuitively causes the laser beam to spread out less, thus enhancing the beam’s ability to maintain its intensity over longer distances.
Because of the larger aperture, if the missile-killer laser beam is aimed at the moon, the infrared spot it would make on the surface would only be about 1.5 miles across. For comparison, the incredibly dim red dot from your pocket laser pointer would be 8 miles wide once it reached the moon.
If you could see in the infrared and stood on the moon underneath the military laser’s beam, it would appear roughly 30 times brighter than the full Earth. That’s quite bright, but not blindingly so. It’s still only one-thousandth the brightness of the midday sun on Earth.
By the time the beam reached the Martians -- if we assume the shortest possible distance between Earth and the red planet, which is about 34 million miles -- the spotlight would be about 200 miles across. Its light should still be noticeable -- about half as bright as the brightest star in the sky sans the sun -- but not exactly attention grabbing.
Looks like we need more power.
The Most Powerful Laser Ever Built:
Several scientific facilities around the world have huge lasers that operate at more than a thousand trillion watts. In other words, these lasers have as much power as a million trillion pocket laser pointers -- that’s almost a billion laser pointers for every person on the planet!
If run continuously, these lasers would use up the entire world's electricity supply in seconds. Luckily, the only reason these lasers can put out such intense power is that they concentrate the release over an extremely short period of time -- usually less than a trillionth of a second. The extremely short laser pulse is then focused down to a point a few thousandths of a millimeter across and can be 10 trillion, trillion times brighter than the surface of our sun. It's so powerful that scientists are using them to rip apart empty space itself in a quest to learn more about the fundamental laws of our universe.
What if we just want to use this for fun and shoot it at space invaders? One major drawback is that these lasers usually produce ultraviolet light, which is mostly absorbed by the Earth’s atmosphere. If we don’t want to turn our air into plasma, we’d have to construct our building-sized super laser cannon in space instead.
Laws of Light and The Inverse Square Law by Jeffrey R.S. Brownson: Laser Light Concentration Decreases Exponentially with Distance
Light intensity decreases with distance from source to receiving surface (sink), and the rate of decrease is in proportion to the square of the distance between emitter and receiver. This is called the Inverse Square Law. The inverse square law for electromagnetic radiation describes that measured light intensity is inversely proportional to the distance squared () from the source of radiation. You might also think of the Inverse Square Law as being analogous to a volume knob on a speaker system, the intensity is turned down, without affecting the pitch of the music. As such, the Inverse Square Law does not affect the wavelengths of light being emitted from the source surface (like the Sun), and so the shape and position of the curve does not change from left to right. Rather, a change in distance between the emitting and incident surfaces will shift the curve directly up or down.
The reasoning for the inverse square law is geometric in nature. As light is emitted from a point (or sphere) like from the Sun and travels toward a receiving surface, the initial quantity of photons is spread out over an increasingly larger spherical area with distance. We can envision the areal spread with increasing distance like an inflating balloon surface. Additionally, the photons from a spherical object like the Sun are emitted in all directions. Now, the surface area of a sphere can be determined in units of distance squared, right? So, the same quantity of photons is contained within a much larger spherical surface area, effectively decreasing the irradiance on the growing surface by “diluting” the photon density.
Dust and Debris on the Retroreflector on the Moon
Additionally, these Retroreflectors on the Moon were said to have been left there by the Apollo mission 50 years ago. That’s 50 years of thousands of micro-debris hitting the Moon, and whatever perturbances might happen on the Moon which would layer the Retroreflectors in a thick coating of opaque crust even after a few years, thereby completely nullifying all reflective properties as well as the silly Retroreflector story. (Where did all the craters on The Moon come from?…evidently things are or were impacting the Moon constantly and stirring things up…)
Finally, there is no empirical proof that there even are Retroreflectors on the Moon, other than hearsay, legend, and fable (In other words: NASA).
Nobody has ever seen these alleged Retroreflectors on the Moon. They are merely inferred to exist because some Elite Scientism Priests have reported that they have identified them with their laser tests. I have already pointed to the absurdity of such long-range laser test reports. In court, these reports would fail based upon the questionable merits of the evidence.
Atmospheric Distortion
Ultimately, various atmospheric distortions resulting from The Earth’s atmosphere, including its seven atmospheric layers, debris, pollution, electromagnetic fields, and atmospheric vapor, would significantly alter the path of any laser beam as it travelled to The Moon and back.
Further, there is no credible evidence coming out of NASA that they are avoiding atmospheric distortion by shooting a laser from the ISS (orbiting at a mind melting 17,600 mph in Low Earth Orbit) at the Moon and then, in turn, capturing that laser light for analysis as the ISS whizzes by at 49 miles per second. The ISS is said to orbit the Earth once every 92 minutes. That’s fast!!! It would have to lock onto a target one foot across, the Retroreflectors on the Moon, and perform this long-distance reflection test from 294,000 miles away, whizzing by at 17,600 mph.
I know NASA thinks the bigger the numbers and more fantastic the story is the more we will believe it, but sorry NASA, I know Star Trek creator, Gene Rodenberry, was a Freemason, and Freemasons and Freemason affiliates were the only astronauts who allegedly went to the Moon. And so, the Retroreflectors on the Moon Theory reads like one of Star Trek’s worst television scripts, and is, more than likely, the result of poor scriptwriting rather than an actual scientific endeavor.
Angle of Incidence, Beam Refraction, and The and Seven Layers of The Earth’s Atmospheric Density
The Earth is allegedly surround by seven layers of atmospheric density, of varying opaqueness and electrometric properties. These layers act as a lens of sorts that bends any laser light passing though it the same way laser light bends at the angle of incidence when going from one medium to another denser medium, as we see when a laser is shot from the air above into the water below. The laser beam bends as it refracts though the water at the angle of incidence.
Atmospheric Density is a measure of how tightly a certain amount of matter is packed into a given volume. The more the stuff is packed in, the higher the density. Density can be calculated by dividing an object’s mass by its volume. It is commonly measured in grams per milliliter or grams per cubic centimeter.
The 7 Layers of Earth’s Atmosphere in Order
1. Exosphere
2. Ionosphere
3. Thermosphere
4. Mesosphere
5. Ozone Layer
6. Stratosphere
7. Troposphere
8. Earth's Surface
Angle of Incidence and Refraction of Laser Beams Through a Medium
In geometric optics, the angle of incidence is the angle between a ray incident on a surface and the line perpendicular to the surface at the point of incidence, called the normal. The ray can be formed by any wave: optical, acoustic, microwave, X-ray and so on. The angle of incidence at which light is first totally internally reflected is known as the critical angle. The angle of reflection and angle of refraction are other angles related to beams. Determining the angle of reflection with respect to a planar surface is trivial, but the computation for almost any other surface is significantly more difficult.
In physics, refraction is the change in direction of a wave passing from one medium to another or from a gradual change in the medium. Refraction of light is the most commonly observed phenomenon, but other waves such as sound waves and water waves also experience refraction. How much a wave is refracted is determined by the change in wave speed and the initial direction of wave propagation relative to the direction of change in speed.
In Summary
And so, as I said, various atmospheric distortions resulting from The Earth’s atmosphere, including its seven atmospheric layers, debris, pollution, electromagnetic fields, and atmospheric vapor, would significantly alter the path of any laser beam as it travelled to The Moon and back. However, a Moon that is 3000 miles away and locally situated inside the Earth’s atmosphere corrects all the aforementioned issues and allows for Lunar Laser Ranging to occur. However, we have never been to The Moon, and so, all of this is absolute NASA nonsense.
Lunar Laser Ranging Experiments
Wikipedia:
Lunar Laser Ranging (LLR) is the practice of measuring the distance between the surfaces of the Earth and the Moon using laser ranging. The distance can be calculated from the round-trip time of laser light pulses travelling at the speed of light, which are reflected back to Earth by the Moon's surface or by one of five retroreflectors installed on the Moon. Three were installed during the Apollo program (11, 14, and 15) and two on the Lunokhod 1 and 2 missions.
Although it is possible to reflect light or radio waves directly from the Moon's surface (a process known as EME), a much more precise range measurement can be made using retroreflectors, since because of their small size, the temporal spread in the reflected signal is much smaller.
A review of Lunar Laser Ranging is available.
Laser ranging measurements can also be made with retroreflectors installed on Moon-orbiting satellites such as the LRO.
History
The first successful lunar ranging tests were carried out in 1962 when Louis Smullin and Giorgio Fiocco from the Massachusetts Institute of Technology succeeded in observing laser pulses reflected from the Moon's surface using a laser with a 50J 0.5 millisecond pulse length. Similar measurements were obtained later the same year by a Soviet team at the Crimean Astrophysical Observatory using a Q-switched ruby laser.
Shortly thereafter, Princeton University graduate student James Faller proposed placing optical reflectors on the Moon to improve the accuracy of the measurements. This was achieved following the installation of a retroreflector array on July 21, 1969 by the crew of Apollo 11. Two more retroreflector arrays were left by the Apollo 14 and Apollo 15 missions. Successful lunar laser range measurements to the retroreflectors were first reported on Aug. 1, 1969 by the 3.1 m telescope at Lick Observatory. Observations from Air Force Cambridge Research Laboratories Lunar Ranging Observatory in Arizona, the Pic du Midi Observatory in France, the Tokyo Astronomical Observatory, and McDonald Observatory in Texas soon followed.
The uncrewed Soviet Lunokhod 1 and Lunokhod 2 rovers carried smaller arrays. Reflected signals were initially received from Lunokhod 1 by the Soviet Union up to 1974, but not by western observatories that did not have precise information about location. In 2010 NASA's Lunar Reconnaissance Orbiter located the Lunokhod 1 rover on images and in April 2010 a team from University of California ranged the array. Lunokhod 2's array continues to return signals to Earth. The Lunokhod arrays suffer from decreased performance in direct sunlight—a factor considered in reflector placement during the Apollo missions.
The Apollo 15 array is three times the size of the arrays left by the two earlier Apollo missions. Its size made it the target of three-quarters of the sample measurements taken in the first 25 years of the experiment. Improvements in technology since then have resulted in greater use of the smaller arrays, by sites such as the Côte d'Azur Observatory in Nice, France; and the Apache Point Observatory Lunar Laser-ranging Operation (APOLLO) at the Apache Point Observatory in New Mexico.
In the 2010s several new retroreflectors were planned. The Moonlight reflector, which was to be placed by the private MX-1E lander, was designed to increase measurement accuracy up to 100 times over existing systems. MX-1E was set to launch in July 2020, however, as of February 2020, the launch of the MX-1E has been canceled. Moonlight will be launched in early 2024 with a Commercial Lunar Payload Services (CLPS) mission.
Principle
The distance to the Moon is calculated approximately using the equation: distance = (speed of light × duration of delay due to reflection) / 2. Since the speed of light is a defined constant, conversion between distance and time of flight can be made without ambiguity.
To compute the lunar distance precisely, many factors must be considered in addition to the round-trip time of about 2.5 seconds. These factors include the location of the Moon in the sky, the relative motion of Earth and the Moon, Earth's rotation, lunar libration, polar motion, weather, speed of light in various parts of air, propagation delay through Earth's atmosphere, the location of the observing station and its motion due to crustal motion and tides, and relativistic effects. The distance continually changes for a number of reasons, but averages 385,000.6 km (239,228.3 mi) between the center of the Earth and the center of the Moon.[20] The orbits of the Moon and planets are integrated numerically along with the orientation of the Moon called physical Libration.
At the Moon's surface, the beam is about 6.5 kilometers (4.0 mi) wide and scientists liken the task of aiming the beam to using a rifle to hit a moving dime 3 kilometers (1.9 mi) away. The reflected light is too weak to see with the human eye. Out of 3.075*10^17 photons (data taken from the apollo website, section "Staggering Odds") aimed at the reflector, only one is received back on Earth, even under good conditions. They can be identified as originating from the laser because the laser is highly monochromatic.
As of 2009, the distance to the Moon can be measured with millimeter precision. In a relative sense, this is one of the most precise distance measurements ever made, and is equivalent in accuracy to determining the distance between Los Angeles and New York to within the width of a human hair.
The Lunar Laser Ranging data is collected in order to extract numerical values for a number of parameters. Analyzing the range data involves dynamics, terrestrial geophysics, and lunar geophysics. The modeling problem involves two aspects: an accurate computation of the lunar orbit and lunar orientation, and an accurate model for the time of flight from an observing station to a retroreflector and back to the station. Modern Lunar Laser Ranging data can be fit with a 1 cm weighted rms residual.
· The center of Earth to center of Moon distance is computed by a program that numerically integrates the lunar and planetary orbits accounting for the gravitational attraction of the Sun, planets, and a selection of asteroids.[32][21]
· The same program integrates the 3-axis orientation of the Moon called physical Libration.
The range model includes:
· The position of the ranging station accounting for motion due to plate tectonics, Earth rotation, precession, nutation, and polar motion.
· Tides in the solid Earth and seasonal motion of the solid Earth with respect to its center of mass.
· Relativistic transformation of time and space coordinates from a frame moving with the station to a frame fixed with respect to the solar system center of mass. Lorentz contraction of the Earth is part of this transformation.
· Delay in the Earth’s atmosphere.
· Relativistic delay due to the gravity fields of the Sun, Earth, and Moon.
· The position of the retroreflector accounting for orientation of the Moon and solid-body tides.
· Lorentz contraction of the Moon.
· Thermal expansion and contraction of the retroreflector mounts.
Results
Lunar laser ranging measurement data is available from the Paris Observatory Lunar Analysis Center the International Laser Ranging Service archives, and the active stations.
Some of the findings of this long-term experiment are:
Properties of the Moon
· The distance to the Moon can be measured with millimeter precision.
· The Moon is spiraling away from Earth at a rate of 3.8 cm/year. This rate has been described as anomalously high.
· The fluid core of the Moon was detected from the effects of core/mantle boundary dissipation.]
· The Moon has free physical librations that require one or more stimulating mechanisms.
· Tidal dissipation in the Moon depends on tidal frequency.
· The Moon probably has a liquid core of about 20% of the Moon's radius. The radius of the lunar core-mantle boundary is determined as 381±12 km.
· The polar flattening of the lunar core-mantle boundary is determined as (2.2±0.6)×10−4
· The free core nutation of the Moon is determined as 367±100 yr.
· Accurate locations for retroreflectors serve as reference points visible to orbiting spacecraft.
Gravitational Physics
· Einstein's theory of gravity (the general theory of relativity) predicts the Moon's orbit to within the accuracy of the laser ranging measurements.
· Gauge freedom plays a major role in a correct physical interpretation of the relativistic effects in the Earth-Moon system observed with LLR technique.
· The likelihood of any Nordtvedt effect (a hypothetical differential acceleration of the Moon and Earth towards the Sun caused by their different degrees of compactness) has been ruled out to high precision, strongly supporting the strong equivalence principle.
· The universal force of gravity is very stable. The experiments have constrained the change in Newton's gravitational constant G to a factor of (2±7)×10−13 per year.