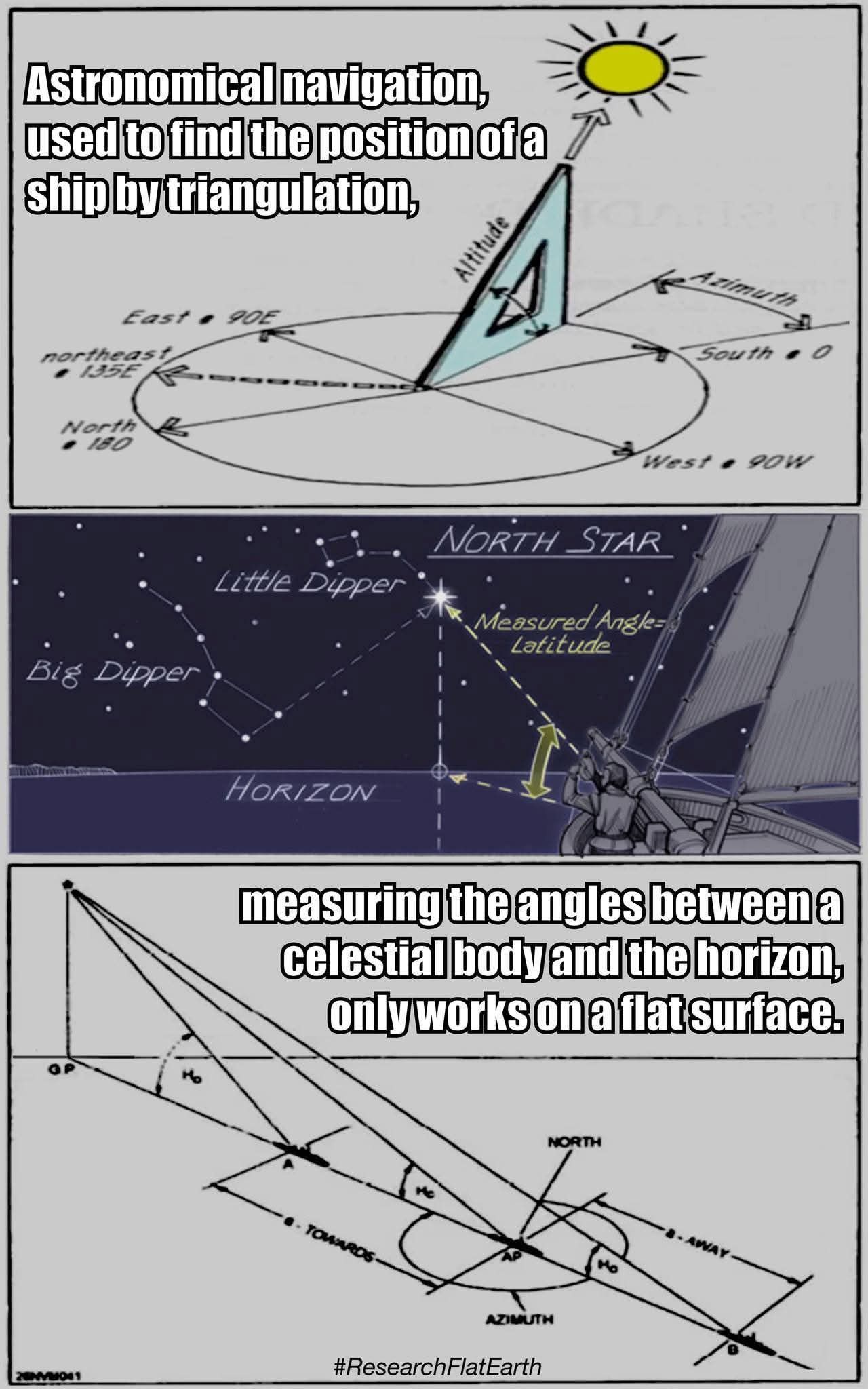
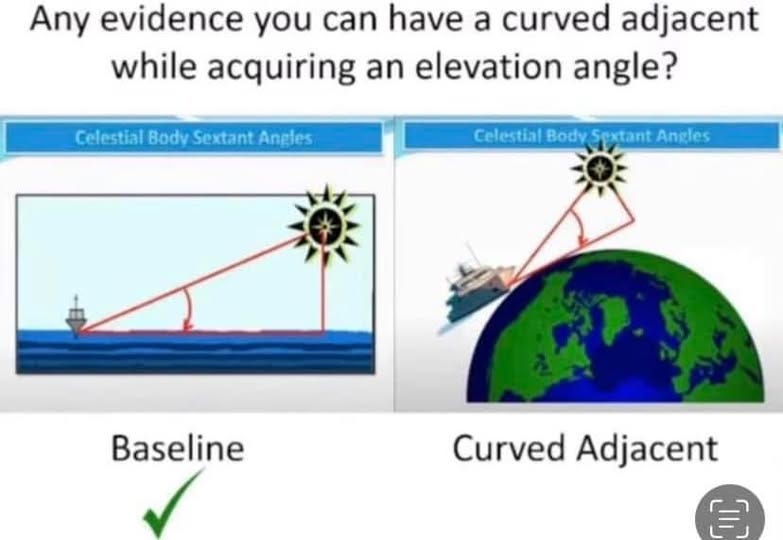
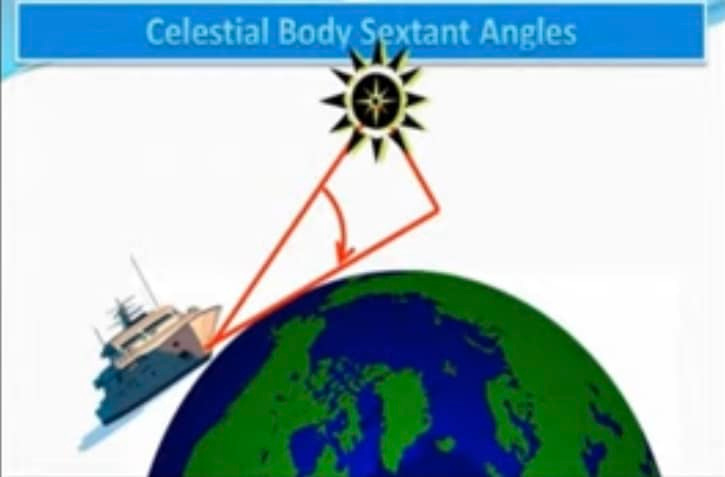
A marine sextant uses a flat baseline for its angles. A spherical Earth does not have a flat baseline, and thus, cannot be used for Celestial Navigation, but must be applied secondarily via spherical trigonometric calculation translations, ensuing the use of a Flat Earth. The whole methodology requires a Flat Earth. With a marine sextant, and before Dip Correction, you measure an angle between the observer’s line of sight to a chosen celestial body, generally The Sun by day and Polaris by night, for example, and you also measure an angle from the observer’s line of sight, holding the sextant at eye height, to the line at the visible horizon, also called the apparent or sensible horizon. This is accomplished from the observer’s eye position on a ship.
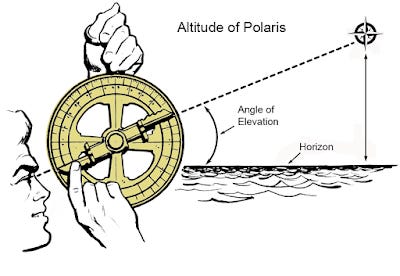
Then, in order to find your desired angle of elevation for your calculations, you need to correct for height of eye above sea level. An “angle of elevation” is the angle between the horizontal and a line of sight to the celestial object above the horizontal, and a sextant is used to measure this angle by using mirrors to align the sight of an object with the horizon. With a sextant, the term for “the horizontal” is the sensible horizon (the plane perpendicular to a navigator’s “zenith”), which is a point directly overhead the navigator, 90 degrees from the horizon. It is crucial for celestial navigation because the zenith distance (the angle between a celestial body and the zenith) can be calculated and used to determine a ship’s position. Sextant measurements are often taken of the celestial body’s altitude (angle above the horizon), and this is then used to find the zenith distance by subtracting the altitude from 90 degrees.
However, a sextant cannot use the sensible horizon directly for celestial navigation. It relies on the visible horizon on the ocean surface, which requires a correction known as Dip Correction. Dip Correction in sextants is the adjustment needed to account for the fact that an observer’s eye is above sea level, which causes the visible horizon to appear lower than the true horizon. This makes the measured angle (sextant altitude) too large, so the Dip Correction, a negative value, must be subtracted from the reading to find the apparent altitude. This correction is determined by the observer’s height of eye above the water and is typically found using tables in a Nautical Almanac or calculated with a formula.
Then, to measure The Sun’s apparent elevation, for example, a user aligns The Sun’s reflected image with the horizon viewed directly, and the angle measured on the sextant scale will be double the angle of elevation (the angle between the horizontal and a line of sight to the celestial object above the horizontal). Once you’ve removed your height of eye using Dip Correction, the angle to your celestial point becomes translated as if having been placed upon the ocean’s surface beneath the ship, which requires a flat horizontal baseline, of course, something that The Globe Model lacks.
Celestial Navigation is only possible on a Flat Earth:
From The Journal of Geocentric Cosmology: This Algorithm was Written by Dr. Steven Alonzo of the Flat Earth University
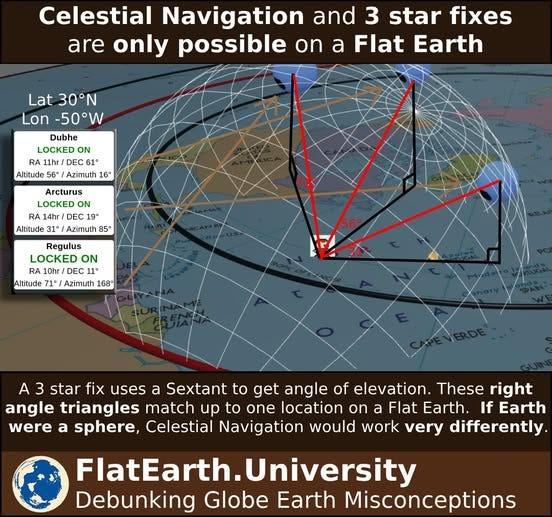
“Our recent submission to the MCToon Sextant Challenge has successfully demonstrated a three-star fix algorithm based on Flat Earth geometry, with the final location of latitude 30 and longitude -50 confirming its precision. By using celestial data from an almanac and a brute-force computational approach, the algorithm accurately calculates the observer’s position based solely on the angle of elevation of stars, without requiring spherical trigonometry. This process offers a compelling proof of concept for celestial navigation on a Flat Earth.
Why This Method Works Without Spherical Trigonometry:
In this Flat Earth model, there’s no need for spherical trigonometry because the curvature of the Earth is not a factor. The algorithm treats the sky as a flat plane, using basic geometry to calculate angles and positions. This simplifies the process significantly, as the complex adjustments required for a spherical Earth (such as dip corrections and great circle calculations) are not needed.”
MCToon Sextant Challenge Attempt 1:
Successfully Completing the MCToon Sextant Challenge on Attempt 2:
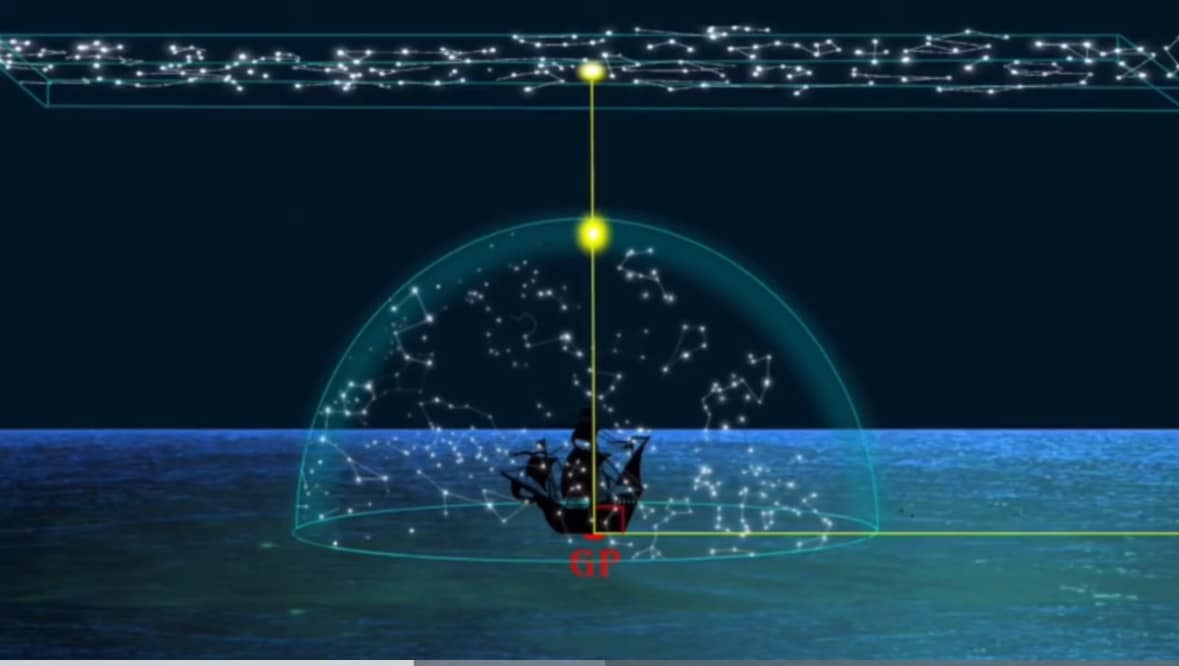
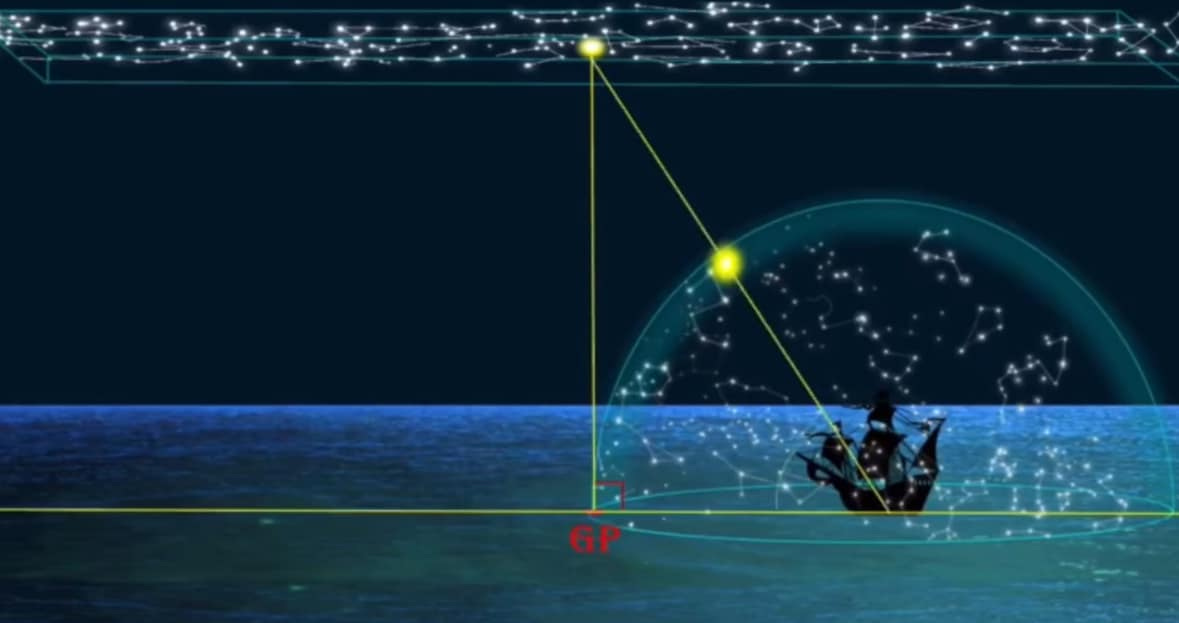
Geographic Position (GP) and Marine Sextants
In the context of celestial navigation using a sextant, GP stands for Geographic Position. It is the single point on the Earth’s surface directly beneath a celestial body (The Sun, Moon, or a Star) at a specific moment in time.
How the sextant and GP are related:
A sextant does not directly measure your position, but rather the angular altitude of a celestial body above the horizon. This measurement is then used to determine your distance from the celestial body’s GP.
Here’s how the process works:
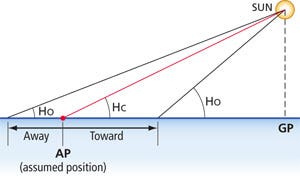
Find the GP: Using an accurate clock and a nautical almanac, a navigator can determine the precise latitude (Declination) and longitude (Greenwich Hour Angle) of a celestial body’s GP at the exact moment a sextant reading is taken.
Measure Altitude: The sextant is used to measure the angle between the celestial body and the visible horizon.
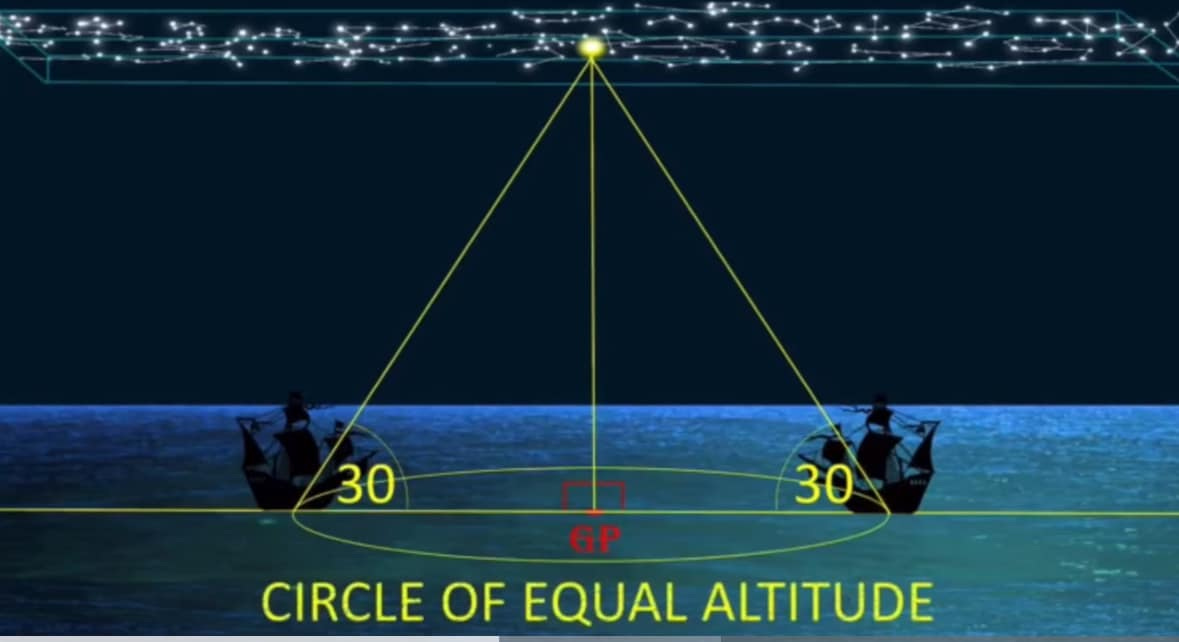
Calculate Distance From GP: The measured altitude angle is directly related to the distance between the navigator’s position and the celestial body’s GP. A key mathematical relationship in celestial navigation is that 1 minute of arc (1/60th of a degree) equals one nautical mile of distance on the Earth’s surface.
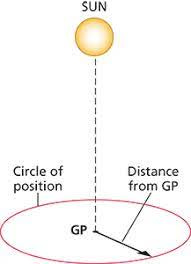
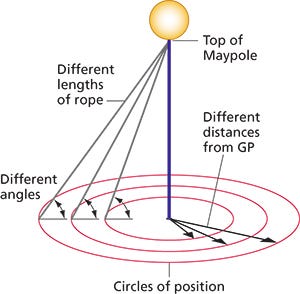
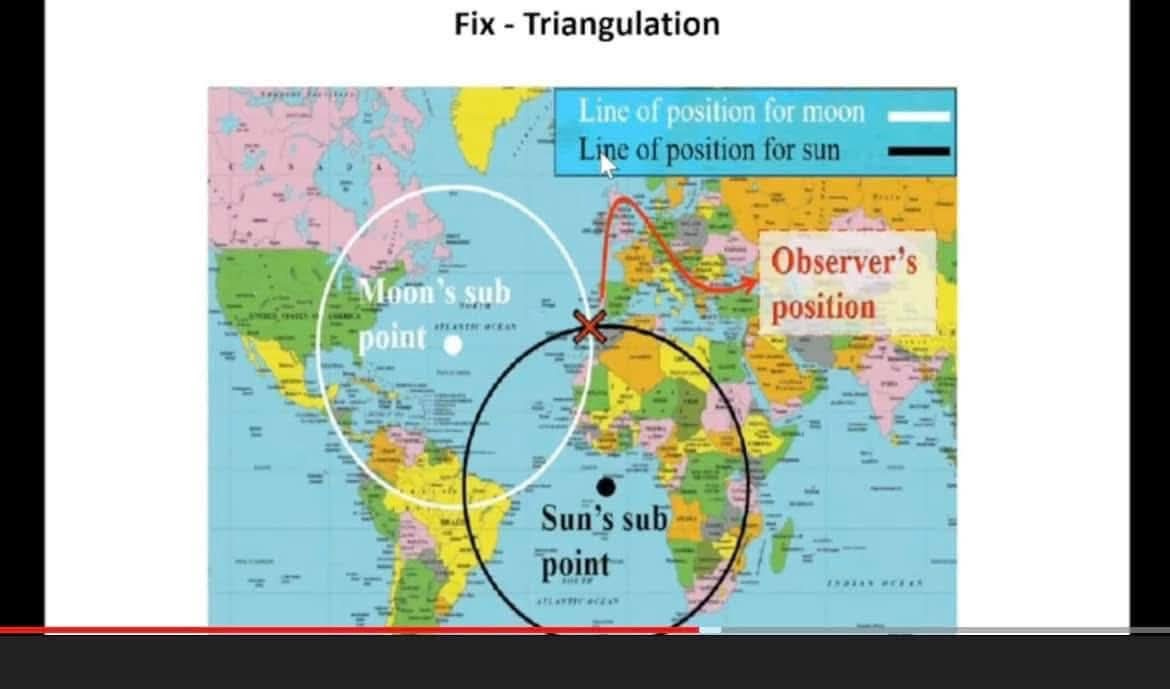
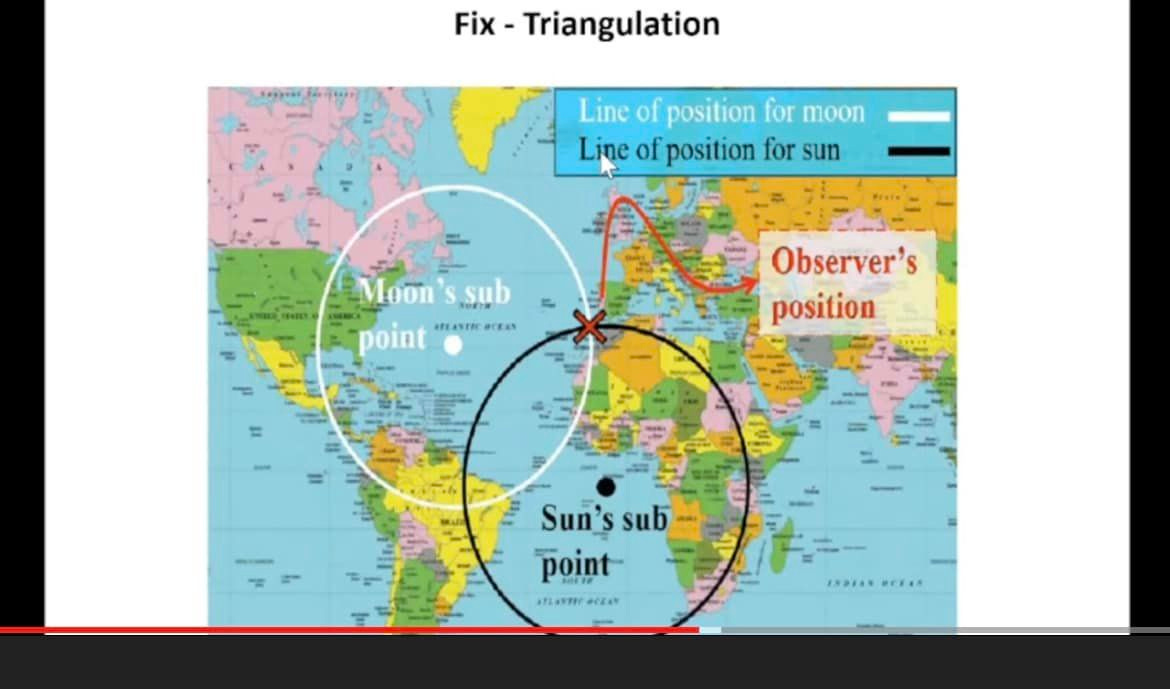
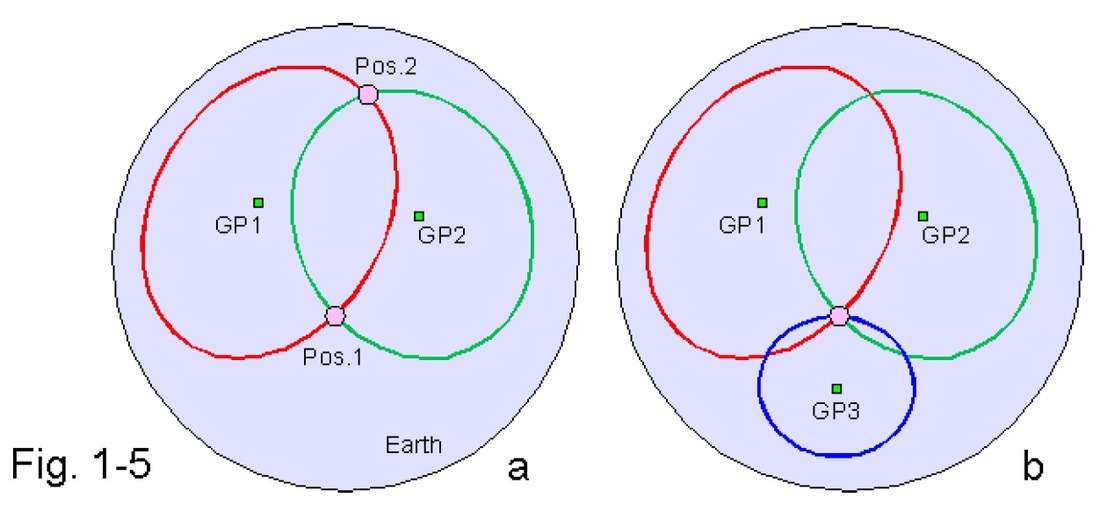
Plot a Line of Position (LOP): A single sextant measurement establishes that the navigator is somewhere on a large circle on the Earth’s surface that is centered on the GP.
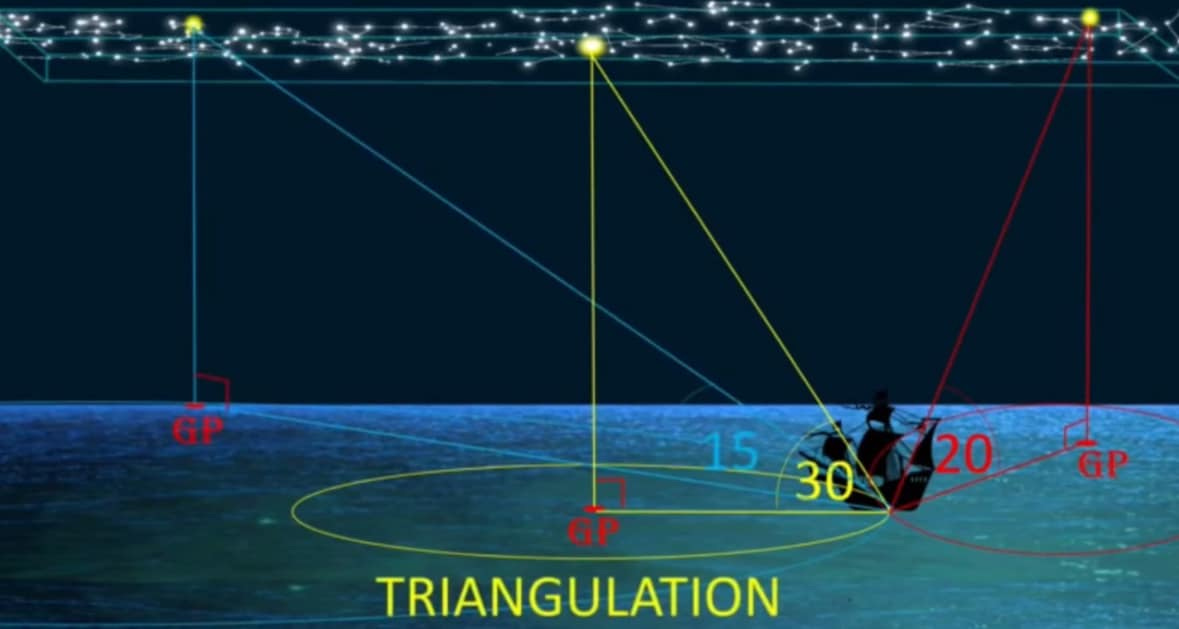
Determine a Fix: By taking sextant readings from at least two different celestial bodies (or the same body at different times), the navigator gets two or more lines of position. The point where these lines intersect is the navigator’s location, known as a “fix”.
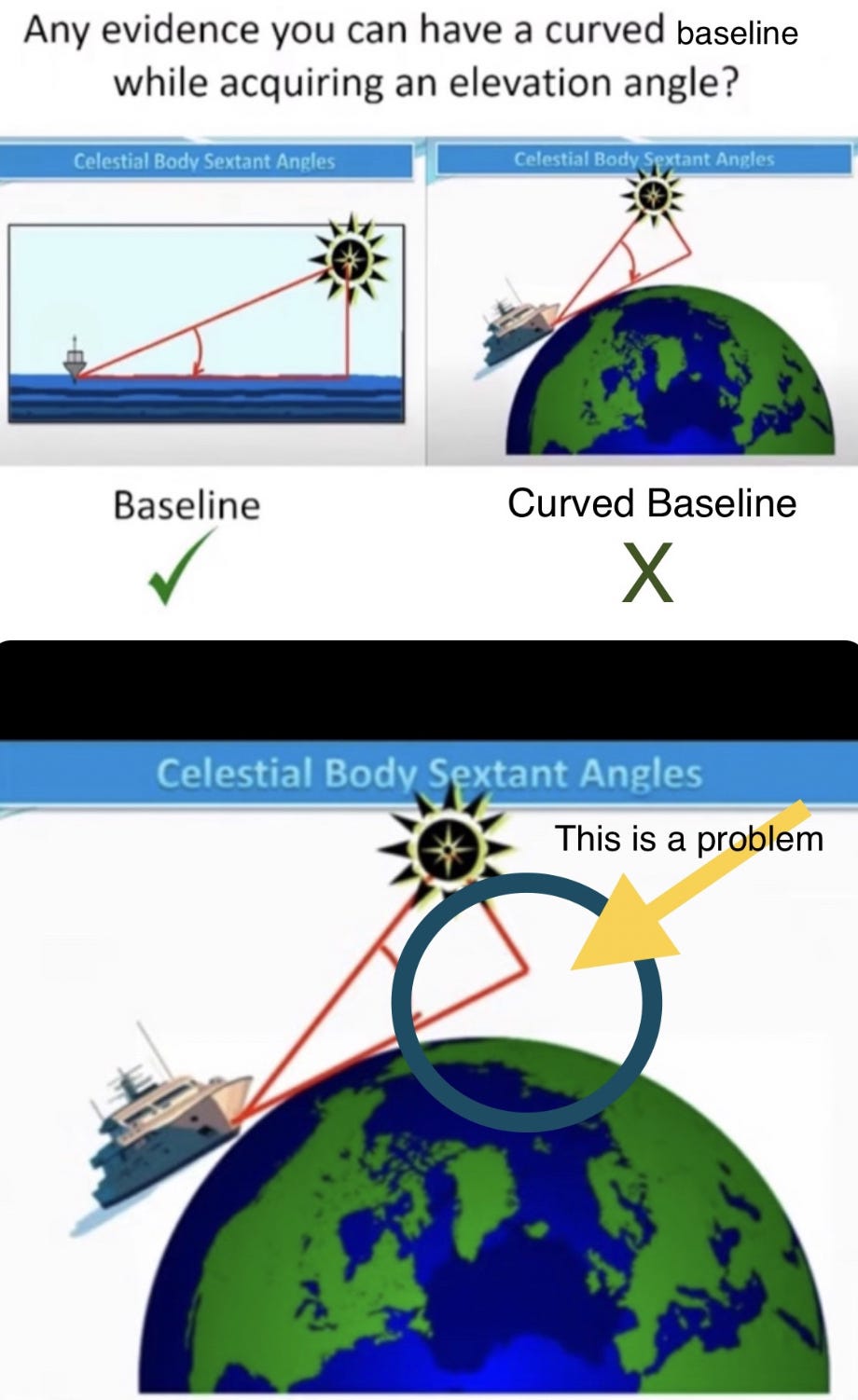
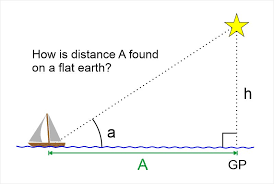
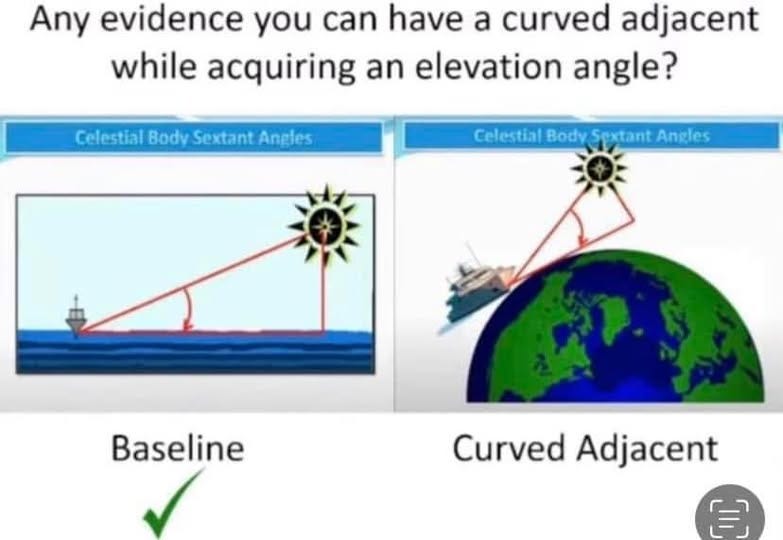
The Necessity of a Flat Earth and Flat Baseline For Celestial Navigation and Sextants
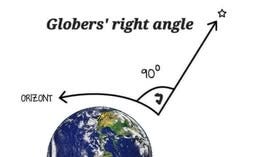
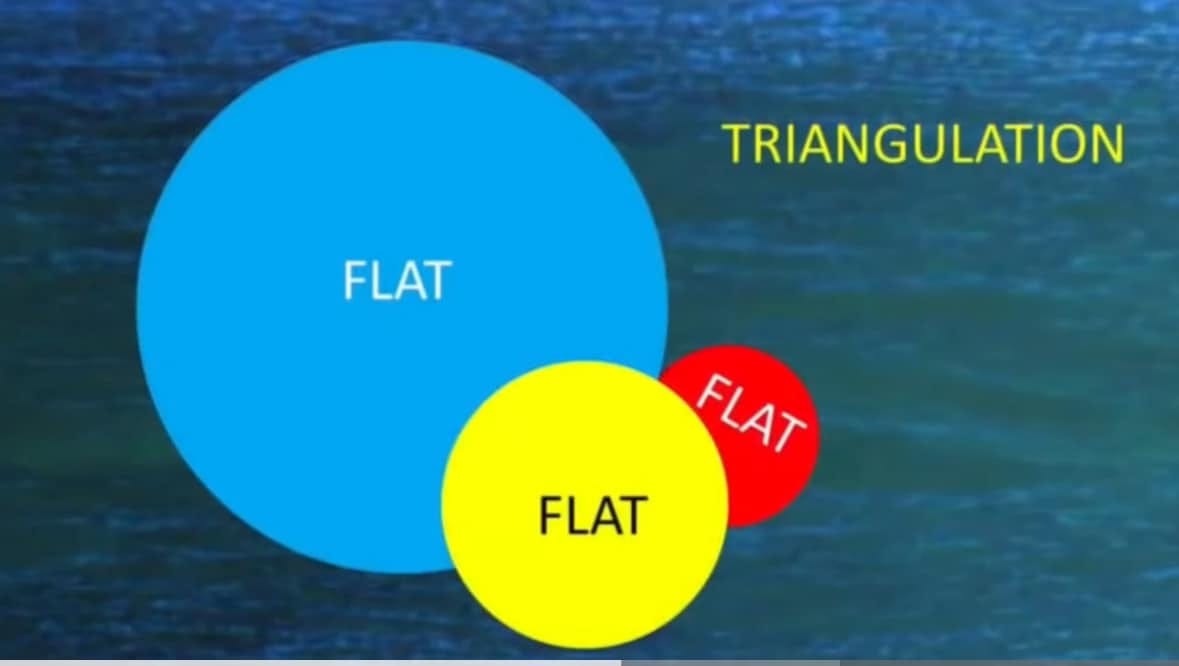
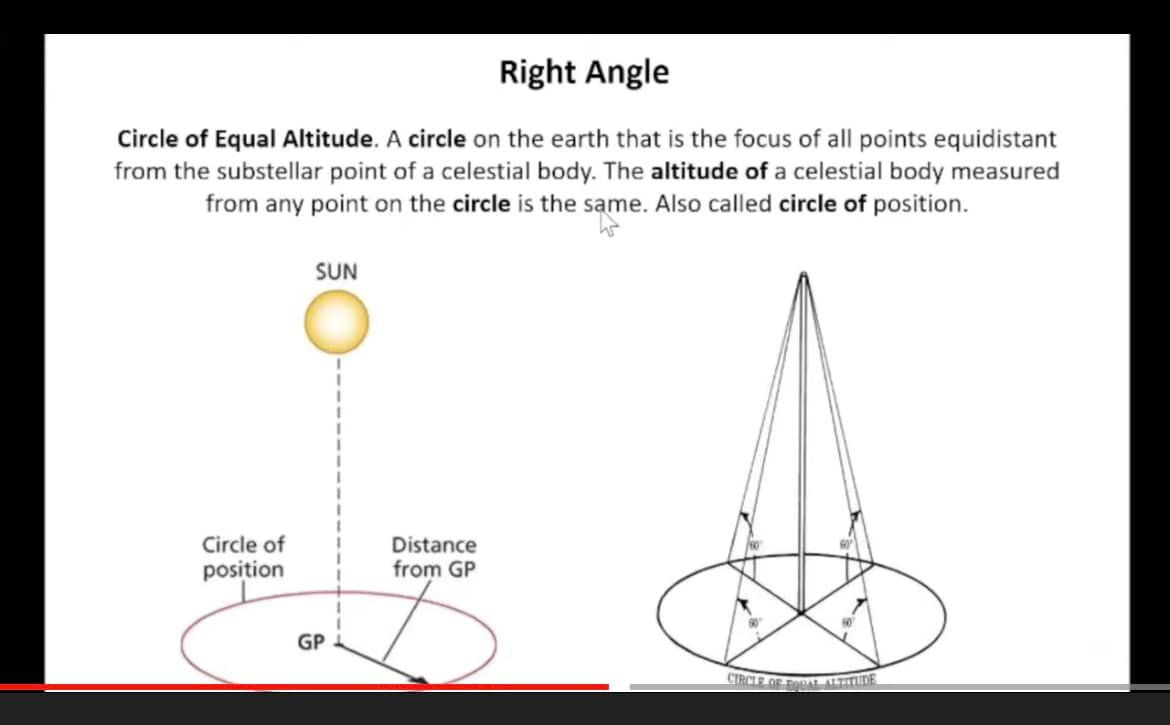
Celestial Navigation and Sextants only work with a flat baseline due to the characteristics of a right triangle. Spherical geometry cannot calculate any accurate elevation angles since it has no flat baseline from the observer to the GP (Ground Position) under The Sun or at night under Polaris. It is crucial to remember that while for the purposes of geometry itself, you can get an elevation angle that is tangent to a sphere, you simply cannot get it for the purposes of Celestial Navigation because a flat baseline is required.
The angle of elevation is the angle between the horizontal line and the line of sight which is above the horizontal line. It is formed when an observer looks upwards at some object above his eye, such as the sky, The Sun, or The Moon. The angle of elevation is a concept related to height and distance, especially in trigonometry.
You also need a flat baseline for your GP (Ground Position) angle. Otherwise, you cannot create a right angle:
Celestial Navigation on Our Flat Earth:
Even the slightest elevation angle error destroys the calculations. After 10 miles of baseline, you’ve already corrupted your entire right triangle integrity...hence the reason a spherical Earth can’t work for Sextant calculations. A flat plane is always assumed by navigators, and only later are spherical geometry calculations superimposed upon this flat plane in order to arrive at a reified (abstract representation) imaginary globe model.
At this height of 231,000 thousand feet, NASA clams we should see over 5,678 feet of curvature. See it?
Celestial Navigation:
Celestial Navigation, also known as astronavigation, is the practice of position fixing using stars and other celestial bodies that enables a navigator to accurately determine their actual current physical position in space or on the surface of the Earth without relying solely on estimated positional calculations, commonly known as “dead reckoning.” Celestial navigation is performed without using satellite navigation or other similar modern electronic or digital positioning means.
Celestial navigation uses “sights,” or timed angular measurements, taken typically between a celestial body (e.g., the sun, the moon, a planet, or a star) and the visible horizon. Celestial navigation can also take advantage of measurements between celestial bodies without reference to the Earth’s horizon, such as when the Moon and other selected bodies are used in the practice called “lunars” or the lunar distance method, used for determining precise time when time is unknown.
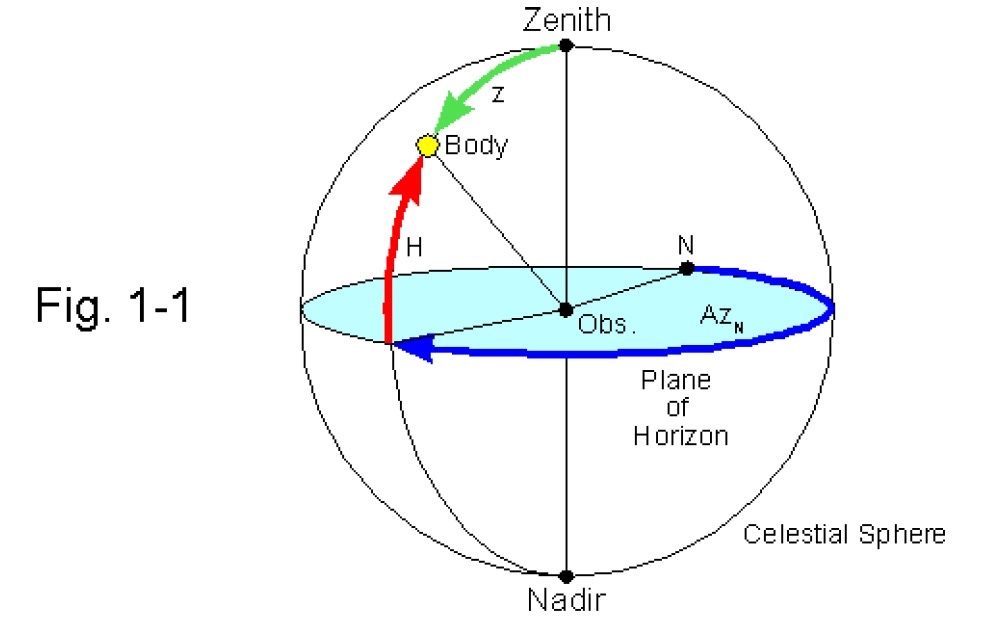
Granted, there is a Celestial Sphere of Stars enveloping the Flat Earth, but The Earth, itself, is a flat plane:
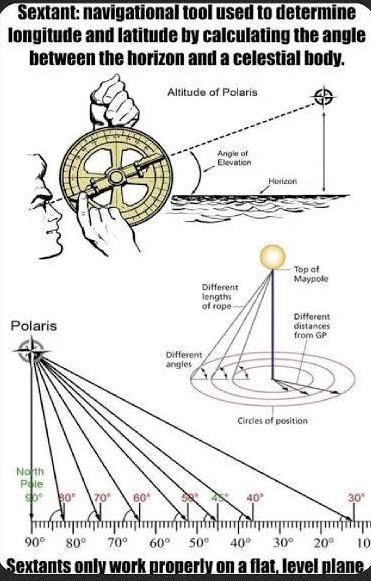
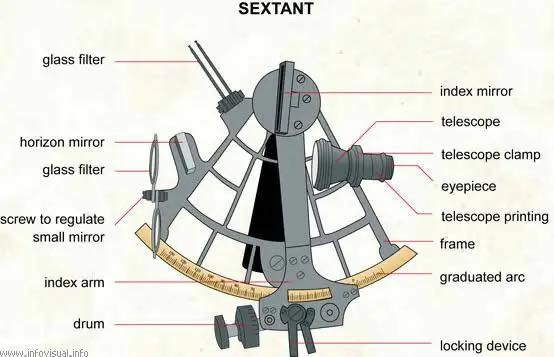
The Sextant:
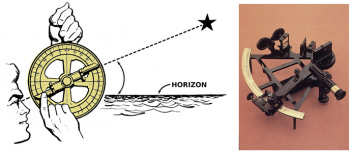
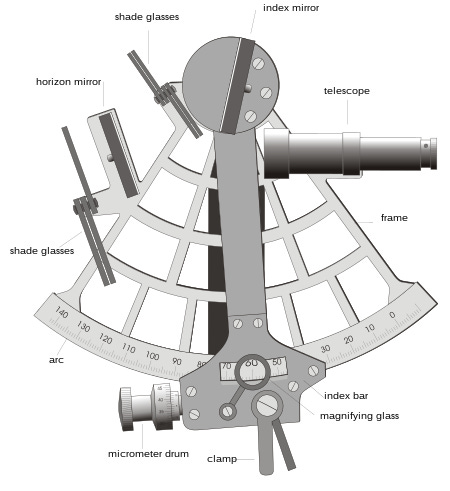
A sextant is a doubly reflecting navigation instrument that measures the angular distance between two visible objects. The primary use of a sextant is to measure the angle between an astronomical object and the horizon for the purposes of celestial navigation.
A diagram of a typical nautical sextant, a tool used in celestial navigation to measure the angle between two objects viewed by means of its optical sight:
The estimation of this angle, the altitude, is known as sighting or shooting the object, or taking a sight. The angle, and the time when it was measured, can be used to calculate a position line on a nautical or aeronautical chart—for example, sighting the Sun at noon or Polaris at night (in the Northern Hemisphere) to estimate latitude (with sight reduction). Sighting the height of a landmark can give a measure of distance off and, held horizontally, a sextant can measure angles between objects for a position on a chart. A sextant can also be used to measure the lunar distance between the moon and another celestial object (such as a star or planet) in order to determine Greenwich Mean Time and hence longitude. The principle of the instrument was first implemented around 1731 by John Hadley (1682–1744) and Thomas Godfrey (1704–1749), but it was also found later in the unpublished writings of Isaac Newton (1643–1727).
More Celestial Navigation Images
Celestial Navigation does not work with a baseline that is only tangent to The Earth because the GP (Ground Position) is not located on a point on The Earth:
Heliocentrists have transposed their flat plane celestial navigation calculations onto a sphere and placed their flat baseline at the center of an imaginary ball Earth, renaming their model, “The Celestial Sphere”:
True Celestial Navigation: