Flat Earth Celestial Navigation Fundamentals
Flat Earth Celestial Navigation Fundamentals 1 demonstrates how angles to the sun across a level surface are converted into distance using nautical miles (nm). This conversion of angles into distances using sextants and almanacs requires an imaginary centre point of an imaginary sphere at a fixed distance from points on the surface (the globe earth projection's assumed radius). The surface is level but the distance is determined by the angle between two points converging at the centre of an imaginary circular earth. This is also how great circle distances are calculated.
This is the first in a series of videos aimed at showing how and why navigation on flat earth is converted into a globe projection. The takeaway from this vid is simply this: Distances in nautical miles across the level earth are interchangeable with angles. 1 degree of sun declination = 60nm.
Proto is Wrong Forever:
Flat Earth Celestial Navigation Fundamentals 1:
In the 2nd in a series of videos, Navigating Flat Earth, we demonstrate and illustrate how celestial navigation is done across flat earth by measuring declination. Support Phuket Word on Patreon: https://www.patreon.com/phuketword Understand how angles and distances are calculated when navigating across flat earth by measuring angles using a sextant and how the angles of declination are converted into an imaginary globe, or distances are considered part of a great circle.
The video is in several parts to explain each step, so DO NOT SKIP, even if you already understand celestial navigation, because this video demonstrates how it is actually done across a level surface and how the declination of luminaries caused by perspective is turned into 360-degree circles in a way that you may not have been shown before.
Do not assume that great circles are slices of a globe. On the contrary. They are flat, circular planes.
Correction: At 46:27, the circle's radius should be 3,400nm, not 5,400.
Flat Earth Celestial Navigation 2:
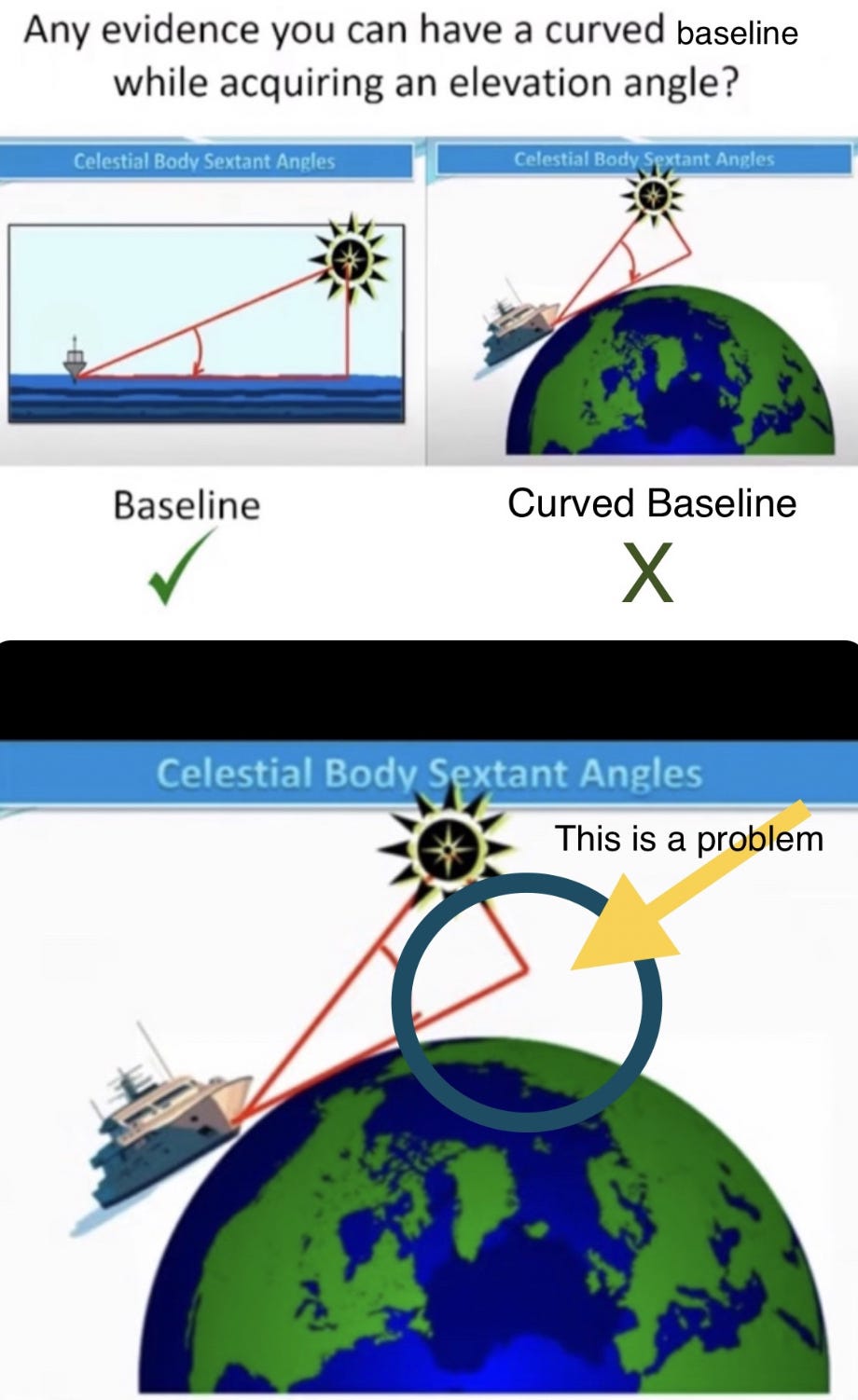
How To Use a Marine Sextant
A marine sextant uses a flat baseline for its angles. A spherical Earth does not have a flat baseline, and thus, cannot be used, but must be applied secondarily via calculation translations after a Flat Earth is used. The whole methodology requires a Flat Earth. With a marine sextant, and before Dip Correction, you measure an angle between the observer’s line of sight to a chosen celestial body, generally The Sun by day and Polaris by night, for example, and you also you measure an angle from the observer’s line of sight, holding the sextant at eye height, to the line at the visible horizon, also called the apparent or sensible horizon. This is accomplished from the observer’s eye position on a ship.
Then, in order to find your desired angle of elevation for your calculations, you need to correct for height of eye above sea level. An “angle of elevation” is the angle between the horizontal and a line of sight to the celestial object above the horizontal, and a sextant is used to measure this angle by using mirrors to align the sight of an object with the horizon. With a sextant, the term for “the horizontal” is the sensible horizon (the plane perpendicular to a navigator’s “zenith”), which is a point directly overhead the navigator, 90 degrees from the horizon. It is crucial for celestial navigation because the zenith distance (the angle between a celestial body and the zenith) can be calculated and used to determine a ship’s position. Sextant measurements are often taken of the celestial body’s altitude (angle above the horizon), and this is then used to find the zenith distance by subtracting the altitude from 90 degrees.
However, a sextant cannot use the sensible horizon directly for celestial navigation. It relies on the visible horizon on the ocean surface, which requires a correction known as Dip Correction. Dip Correction in sextants is the adjustment needed to account for the fact that an observer’s eye is above sea level, which causes the visible horizon to appear lower than the true horizon. This makes the measured angle (sextant altitude) too large, so the Dip Correction, a negative value, must be subtracted from the reading to find the apparent altitude. This correction is determined by the observer’s height of eye above the water and is typically found using tables in a Nautical Almanac or calculated with a formula.
Then, to measure The Sun’s apparent elevation, for example, a user aligns The Sun’s reflected image with the horizon viewed directly, and the angle measured on the sextant scale will be double the angle of elevation (the angle between the horizontal and a line of sight to the celestial object above the horizontal). Once you’ve removed your height of eye using Dip Correction, the angle to your celestial point becomes translated as if having been placed upon the ocean’s surface beneath the ship, which requires a flat horizontal baseline, of course, something that The Globe Model lacks.