David Foster Explains Why Camera Zoom Debunks the Heliocentric Earth Radius Claim

* The Radius Value (R-Value) of The Earth has often been calculated using distance to a physical horizon measurements and relies upon the claim that the horizon is a physical obstruction to any observer’s vantage point across the ocean. This alleged physical obstruction is said to literally be Earth curvature, and as such, it is said to be responsible for obscuring objects such as ships and boats as they navigate on the distant ocean horizon.

*We must always remember that The Radius Value (R-Value) of The Earth is a reified imaginary value that exists only in mathematical modeling but is nowhere to be seen or experienced in actual daily reality. This Radius Value is used to conform to mathematical equations, but has never in any sense been observed, quantified, or witnessed in real time by any observer.    

Nevertheless, as we can see from zoomed photos, any ship or boat that appears to have gone beyond this alleged physical horizon can be brought back into view, thereby proving conclusively that the horizon is not physical at all, but rather, merely apparent. This self-evident lack of curvature at the horizon therefore disproves the claimed Radius Value of The Earth of 3,963 miles.

Daniel Stapleton:

“If you understand perspective, you realize the ship is just beyond the vanishing point instead of under earth curvature. These modern cams kill the ball Earth lie.”

Limited Vision is Not Earth Curve:

Without this claimed Radius Value, the entire mathematical matrix of spherical Earth falls to pieces. Subsequently, with one simple photograph, all the spherical geometry claims of The Heliocentric Model are rendered erroneous and useless.

Contrariwise, once a car goes over a physical hill, no amount of zooming in with a camera will bring the car back into view. That’s because the hill is physical, a curve that actually exists with real topographical characteristics in contradistinction to imaginary Earth curvature on the ocean.

Additionally, even if you factor in refraction into the geometric horizon at 1.23 miles times the square root of the eye height in feet, with the height of the observer at one foot, your new result is only 1.32 miles times the square root of the height in feet. In other words, even with refraction factored into the equation, you still cannot account for why we see things up to 8 miles beyond the imaginary geometric limitation espoused to be Earth curvature.

In a nutshell, what The Heliocentrists are saying is that if you are standing in a valley and a huge hill is obstructing your view of some houses on the other side of the hill, refraction will cause those hidden houses to jump up into your vision, while at the same time, the hill will suddenly become located behind those houses instead infront of them blocking your view, as they initially were. That’s the paradoxical nature of this Heliocentric one-size-fits-all refractory claim.  

                                           --Adapted From David Foster’s Thoughts

David Foster Adds to the Famous Black Swan Argument Which Proves the Globe Deception and The Myth of a Geometric Horizon

David Foster (With My Edits):

So as a Flat Earther I hear a lot about “The Edge of The Earth”. I understand the question and realize it’s very difficult to understand for many that The Edge is like the shore of a lake.

The Flat Earth “Edge”:

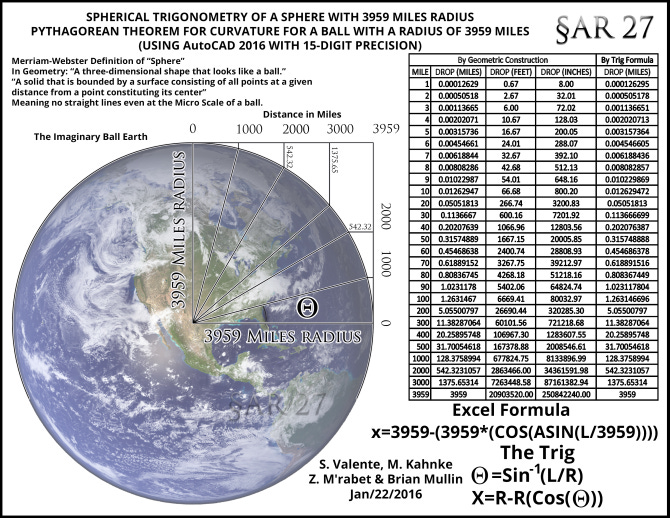
But, let’s put that aside for a moment and talk about “The Globe Edge”, which is supposed to be a visible Geometric Horizon, which is the calculated and expected horizon distance on a globe with a circumference of approximately 24,901.461 miles, which equates to 2.73 miles away from the observer at *5 foot camera height, to this imaginary “edge”, otherwise known as the demarcation point where The Earth is supposed to begin curving away from the observer. In other words, in the Heliocentric Model, this “tangent point” (tangent to the Earth's surface) is called The Geometric Horizon, and it is 2.73 miles from the observer, the physical place where Earth curvature allegedly begins to obfuscate boats and buildings. Again, on a sphere with a radius of 3,959 miles and a circumference of 24,900 miles, there must be a point where the curve begins to obscure things. In fact , this is the crux of the entire Globe Model claim.

*We must always take into account the height of the observer. This is an integral component of the calculations. Without the height of the observation, curvature calculations make no sense.

The Imaginary, Non-Existent Globe Earth “Edge” (The Alleged Earth Curve Start Point):

Now, at a 1 foot camera height, objects must begin to be obscured at 1.22 miles. Otherwise, the math does not work on the sphere. There’s an edge at that distance, again not-so-surreptitiously called Earth curvature, and it must be physical if The Earth was, indeed, a sphere. However, the problem is, there’s thousands of photographs showing that this alleged “edge” (Earth curve) starts at a distance far, far greater than would be possible on a sphere of 24,900 miles in circumference. In fact, the ”edge” that Heliocentrists claim is blocking boats and buildings appears to mathematically correlate to a sphere with a circumference of something more in the magnitude of 250,000 miles in circumference. The reason for this is because we can see many, many miles beyond this mythical 2.73 miles Globe edge, which is supposed to exists by virtue of the spherical geometry calculations required for their Globe circumference specifications.

In the photo below, taken at a 1 foot camera height, we can see 10 to 20 times further than would be possible:

Stated more precisely, The Geometric Horizon, or line at which curvature is expected to be detectable from the observer, is 1.225 square miles times the square root of the observer’s height in feet:

This is the point where the Earth is expected to begin curving away from the observer’s frame of reference. According to The Heliocentric Model, anything beyond this point is expected to be obstructed and hidden behind this “hill” of curvature.

Also, the atmosphere bends (refracts) light that is traveling horizontally. What this usually means is that a ray of light is able to slightly follow the alleged curvature of the Earth, so that the optical horizon is a bit further away than the geometric horizon.

Nevertheless, the refraction due to the atmosphere is neither constant nor predictable, as it depends on the change of temperature with height, which cannot be determined or factored into any expected Earth curvature equations without massive inconsistencies and derivation errors. There is, therefore, no simple way to add a correction to the formula for the geometric horizon, though one may achieve an “average” margin of error correction by assuming a radius for the Earth, 6,378 km (3,963 miles), that is a bit greater than the true radius. However, whatever variable one inserts into the expected curvature/refraction equation, it never correlates with any actual observations made in the real world. It is never correct. It is always some imaginary refraction quotient that does not provide justification for what we actually observe.

This, my fine feathered Globe believers, is famously know as The Black Swan. The Black Swan photo was taken from a video posted by a Flat Earther on his You Tube channel on October 25, 2016. As you can see in the photo, Platform Hillhouse on the right in this photo is 6.21 miles from the place where the video was made, while Platform Habitat on the left is 9.41 miles from where the video was made. The video was made at water’s edge, only a few feet above the water. From this distance and the height of the observer, the Earth’s curvature ought to produce noticeable blockage of the lower parts of either platform, with more of Platform Habitat being blocked due to its greater distance, as well as blocking the apparent Horizon beyond the oil rigs. There appears to be no blockage of either of the platforms, and one can readily see that the horizon is beyond the two platforms. This single image constitutes evidence disproving the Earth is a sphere having 24,000 miles circumference. Flat Earthers argue that this view is expected on a Flat Earth, and so, they correctly concluded that the Earth must be flat. To achieve this line of sight to the apparent Horizon beyond the oil rigs, The Earth would need to have radius of approximately 250,000 miles, which is absolutely not what The Heliocentric Model teaches.

The Black Swan Photo Again:

Hundreds and Hundreds and Hundreds of Miles of Zero Curvature

We Have at Least Four Horizon Line Versions Being Discussed in The Flat Earth Versus Globe Debate:

1. The Geometric Horizon, which is the calculated and expected horizon distance on a globe with a circumference of approximately 24,901.461 miles, which equates to 2.73 miles. In the Heliocentric Model, this “tangent point” (tangent to the Earth's surface) is called the geometric horizon, and it is 2.73 miles from the observer.

2. The Apparent or Optical Horizon, which is the horizon line that we see with the naked eye, but which can be extended and increased using high powered telescopic apparatus.

3. The Actual Horizon, which is the natural compression point of convergence in the distance that naturally occurs on any flat plane do to the principles of perspective, which also effects angular resolution, and is dictated by the inherent limitations of any optical apparatus to resolve anything beyond this natural optical limit, therein.

4. The Refracted and Distorted Horizon, which can be attributed to any combination of various naturally occurring effects, including refraction, atmospheric distortion, and humidity, etc…

The Geometrical Horizon According to Encyclopedia Britannica as Related to the Black Swan

The Geometrical Horizon From Encyclopedia Britannica:

“The intersection of the celestial sphere and an infinite number of straight lines radiating from the eye of the observer and tangent to the Earth's surface.” —Encyclopedia Britannica

The Heliocentrists claim that because of the Earth’s circumference is  approximately 24,901.461 miles, therefore, the geometric horizon is 2.73 miles from the observer, as is derived from spherical geometry using trigonometric math. Hence the Geometric Horizon is the calculated and expected visible horizon distance on a globe with a circumference of approximately 24,901.461 miles, which equates to 2.73 miles.

However, in the famous The Black Swan situation with two oil rigs, the geometric horizon appears at nearly 10 miles away, therefore debunking the claim that The Earth curves away from the observer at 8 inches per mile squared from the observer.  

The thing you need to remember here is that maximum visibility is not about calculating where the horizon is. Instead, it refers to the ability to see and identify a prominent dark object against the sky at the horizon during the day. This is all related to the opacity of the atmosphere. So if it’s a hazy day, a smoggy day, or a rainy day, the visibility will decrease. The horizon is irrelevant in this case.

The Heliocentric Model’s Geometrical Horizon Claim Debunks Earth Curve: The Black Swan:

For a six-foot (182.88 centimeters) tall person, the horizon is a little more than 3 miles (5 kilometers) away. Geometry tells us that the distance of the horizon (i.e. the farthest point the eye can see before Earth curves out beneath our view) depends simply on the height of the observer.

In this model, you can see farther the higher you are in altitude.

Of course, the same applies for The Flat Earth Model, and so it is a moot point.

The Heliocentrists claim that because of the Earth’s circumference is approximately 24,901.461 miles, therefore, the geometric horizon is 2.73 miles from the observer, as is derived from spherical geometry using trigonometric math.

Hence the Geometric Horizon is the calculated and expected visible horizon distance on a globe with a circumference of approximately 24,901.461 miles, which equates to 2.73 miles.  

However, in the famous The Black Swan situation with two oil rigs, the geometric horizon appears at nearly 10 miles away, therefore debunking the claim that The Earth curves away from the observer at 8 inches per mile squared from the observer.

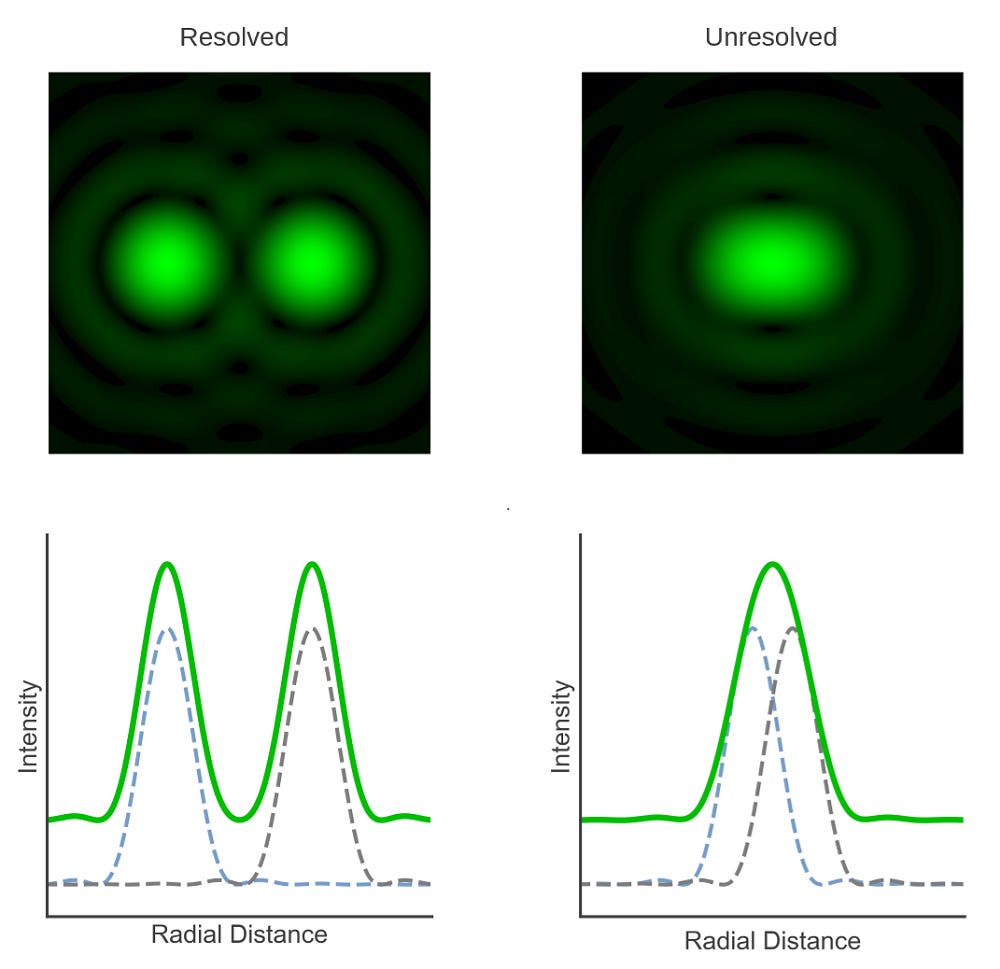
***Note: The distortion on the upper left side of the distant oil rig is NOT due to refraction. It is due to the atmospheric compression that occurs as you get farther and farther out to the tangent point between the horizon and the sky. This effect where distant objects can no longer be fully resolved is known as The Rayleigh Criterion. The Rayleigh Criterion is the generally accepted criterion for the minimum resolvable detail, where the imaging process is said to be diffraction-limited when the first diffraction minimum of the image of one source point coincides with the maximum of another. However, diffraction should not be confused with refraction. We classically think of light as always traveling in straight lines, but when light waves pass near a barrier they tend to bend around that barrier and become spread out. The definition of diffraction is the spreading of waves as they pass through or around an obstacle, which does not make distant objects jump up from the horizon. Rather, it merely makes distant objects less resolvable and distorted. Atmospheric compression and distortion, as predicated by The Rayleigh Criterion, is very common. Nevertheless, you can still see the horizon far beyond the second oil rig (at 9.41 miles), which illustrates that there is no expected Earth curvature in the photo.

The Rayleigh Criterion:

Beyond The Horizon - A Flock of Six Black Swans in a Row:

A Hyper-Condensed Explanation of The Earth Radius Value With Refraction Paradox:

Ultimately, as soon as you say it is refraction that is causing distant objects to distort and/or appear, then you have just destroyed your claim that it is Earth’s curvature or any geometric limitation that is responsible for concealing distant objects. There is no calculation for Earth curve refraction in the Earth curve calculations by Heliocentrists. It’s atmospheric refraction, not Earth curve refraction. In other words, the horizon that we are looking at is a non-geometric refracted position, which is not an Earth curvature proof. Refraction does not block distant objects. It simply refracts light. And so, if you are trying to claim that The Earth’s curvature is blocking your vision of distant objects, and then also saying that far beyond the geometric horizon at 1.23 miles times the square root of the eye height in feet, where we are not supposed to see anything due to Earth curvature, refraction is distorting various images that are supposed to be below this imaginary curve, you have just destroyed your entire claim of Earth curvature. 

You can’t have it both ways.

Additionally, even if you factor in refraction into the geometric horizon at 1.23 miles times the square root of the eye height in feet, your new result is only 1.32 miles times the square root of the height in feet, according to Andrew Thomas Young. In other words, even with refraction factored into the equation, you still cannot account for why we see things up to 8 miles beyond the imaginary geometric limitation espoused to be Earth curvature.

In a nutshell, what The Heliocentrists are saying is that if you are standing in a valley and huge hill is obstructing your view of some houses on the other side of the hill, refraction will cause those hidden house to jump up into your vision, while at the same time, the hill will suddenly become located behind those houses instead infront of them blocking your view, as they initially were. That’s the paradoxical nature of this Heliocentric one-size-fits-all refractory claim.  

Flat Earth Debate 1938 LIVE MC Toon Vs Patrick Gunnels Part Two:

Witsit vs. MCToon Debate: MCToon Eviscerated by Austin Witsit:

MCToon is adept at dancing in the gray area, the unobservable, the nonsensical pseudoscience realm that he dwells within.

Witsit vs. MCToon Debate:

BREAKING NEWS: McToon UNLEASHES Black Swan Globe APOCALYPSE!!!:

Thanks Bob (The Pseudoscience Guy):

The Black Swan Argument?:

7:6R Keeps Destroying the Globe Model:

The Lake Pontchartrain Black Swan:

The thing you need to remember here is that maximum visibility is not about calculating where the horizon is. Instead, it refers to the ability to see and identify a prominent dark object against the sky at the horizon during the day. This is all related to the opacity of the atmosphere. So if it’s a hazy day, a smoggy day, or a rainy day, the visibility will decrease. The horizon is irrelevant in this case.