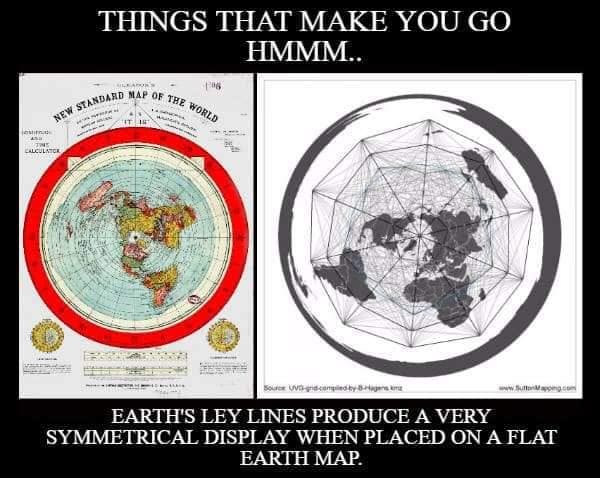
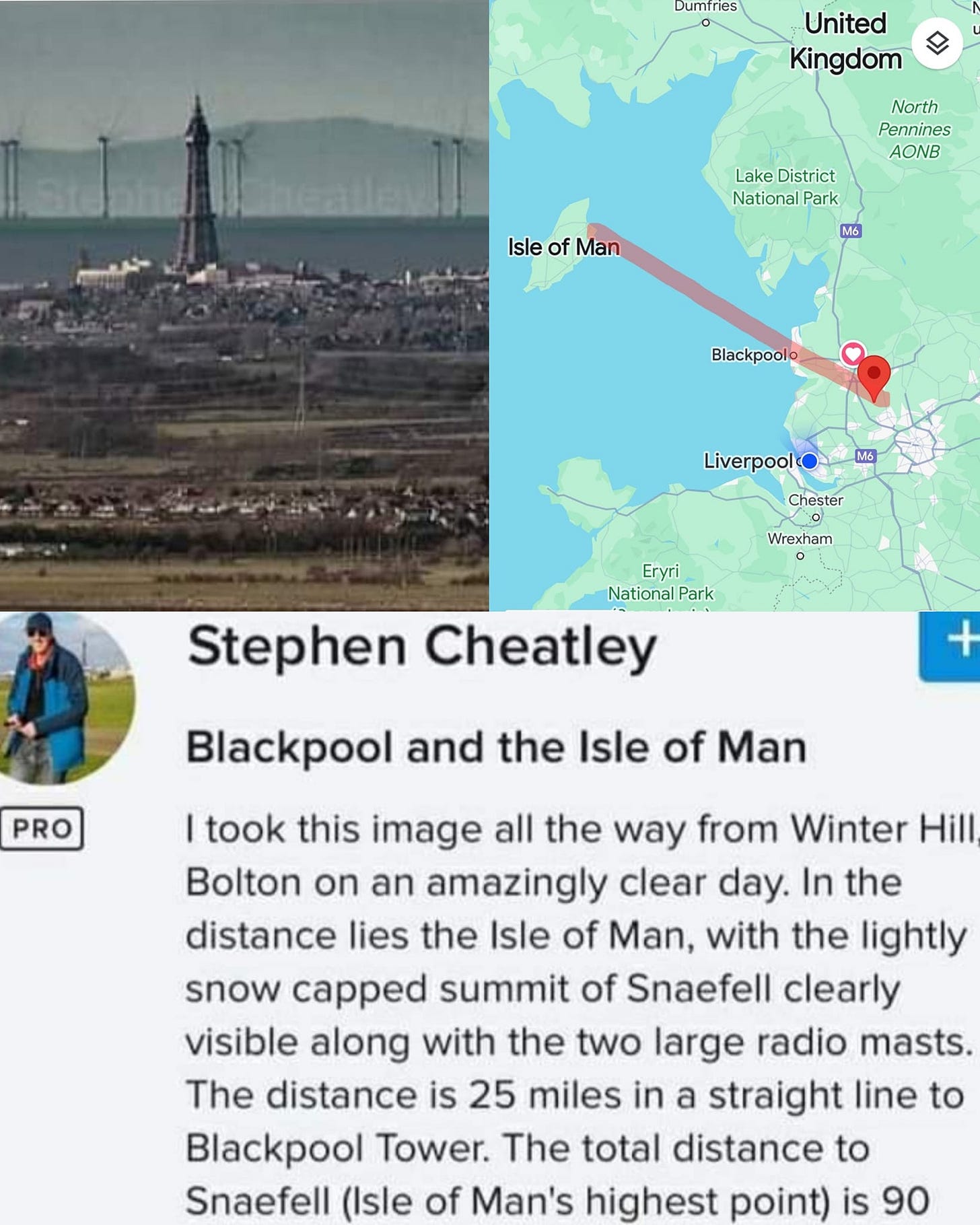
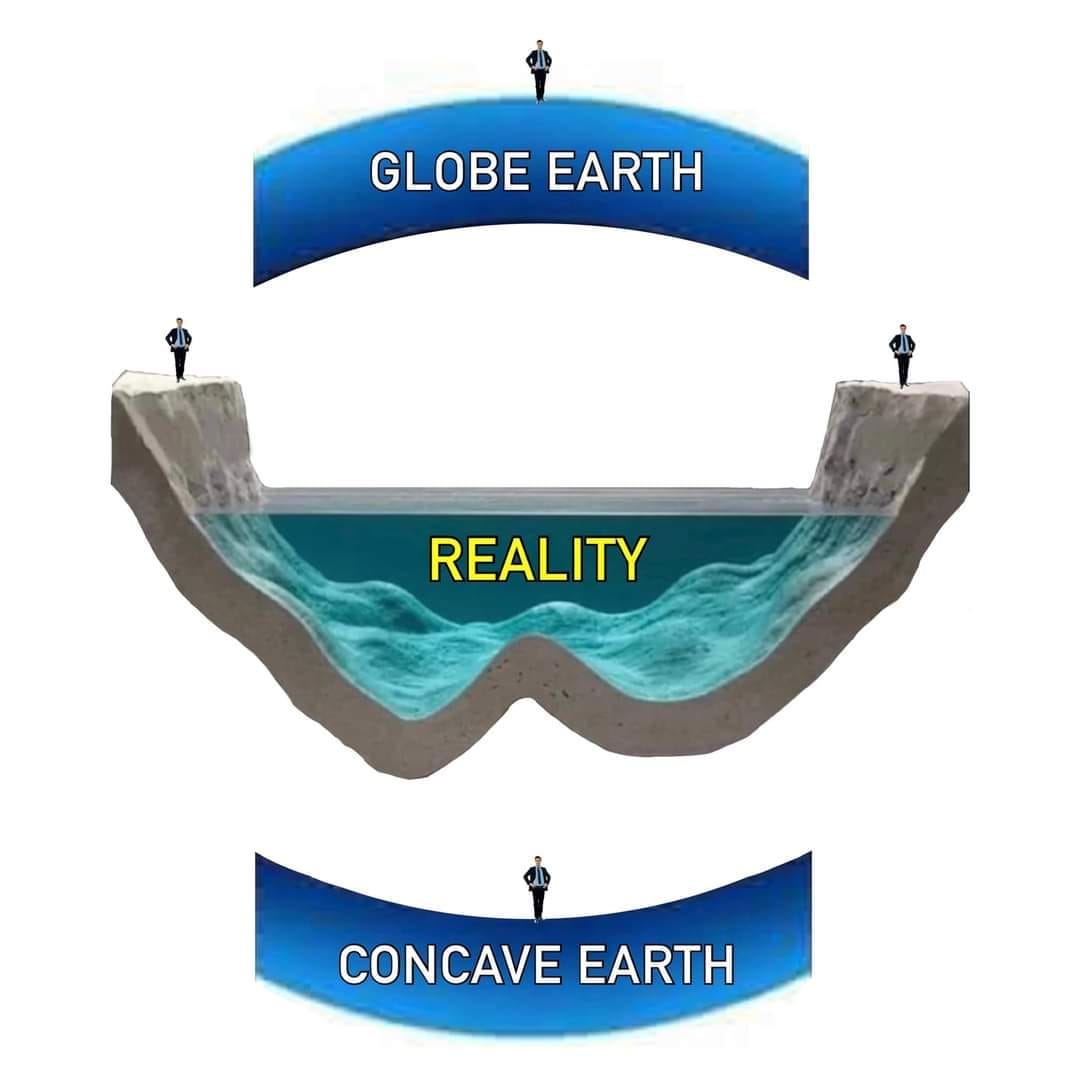
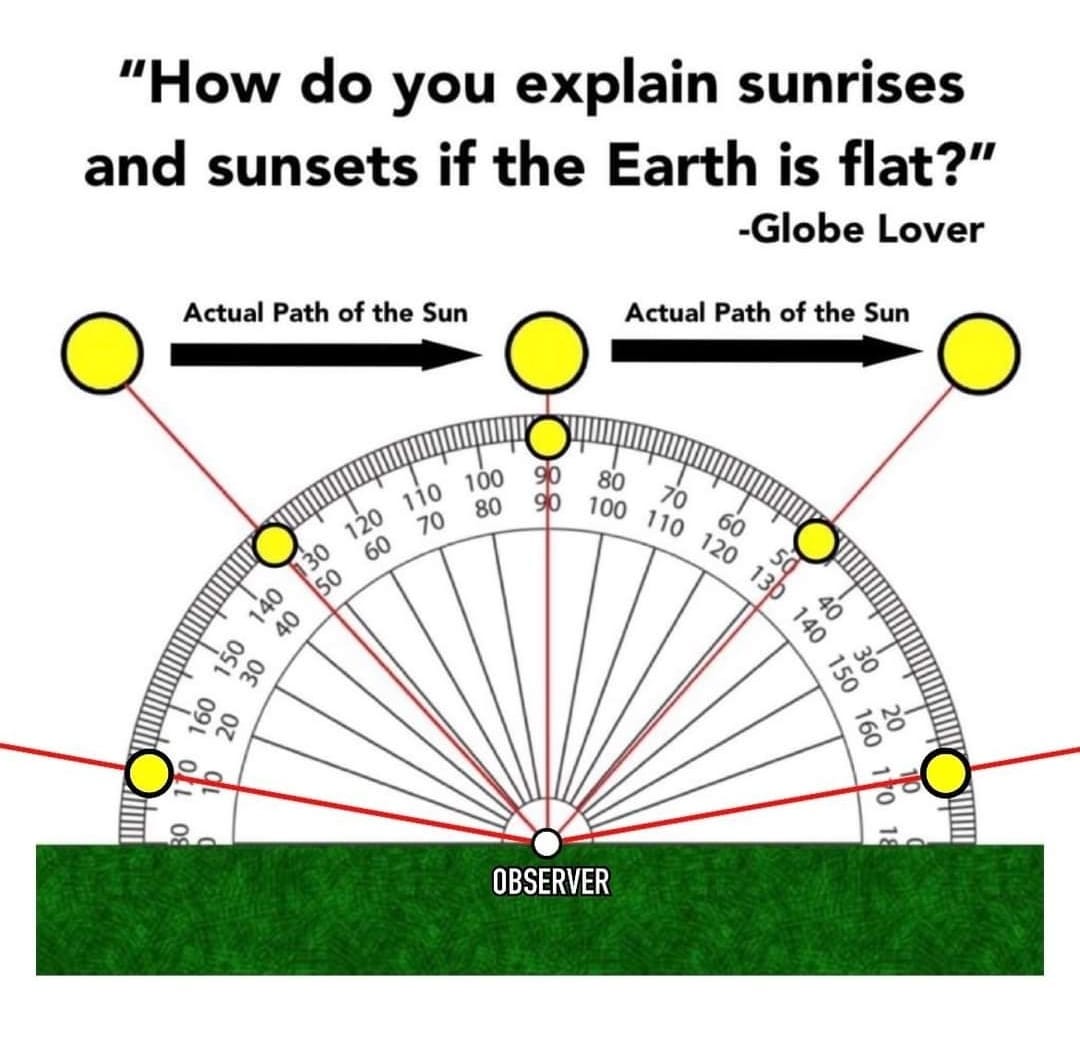
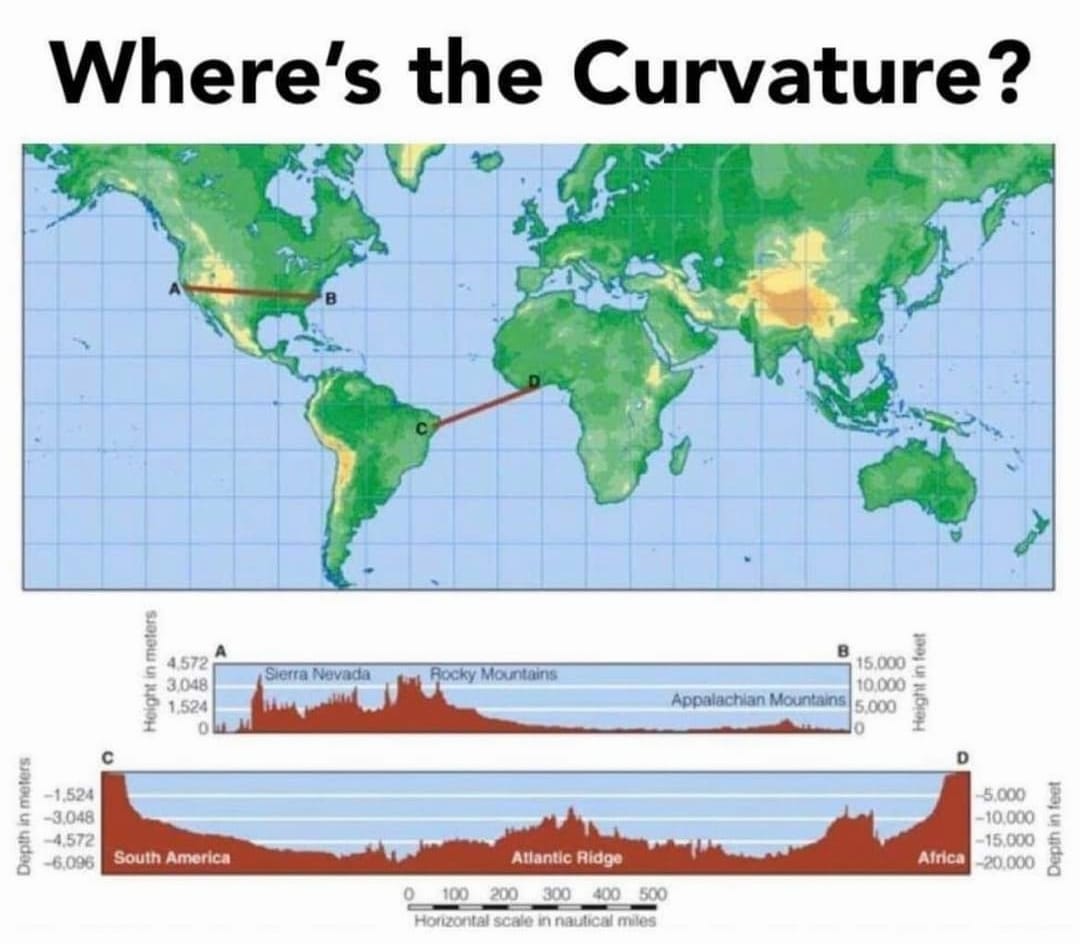
Angular Resolution is Not Considered By Heliocentrists in Earth Curve Calculations: The Role of The Rayleigh Criterion in Angular Resolution
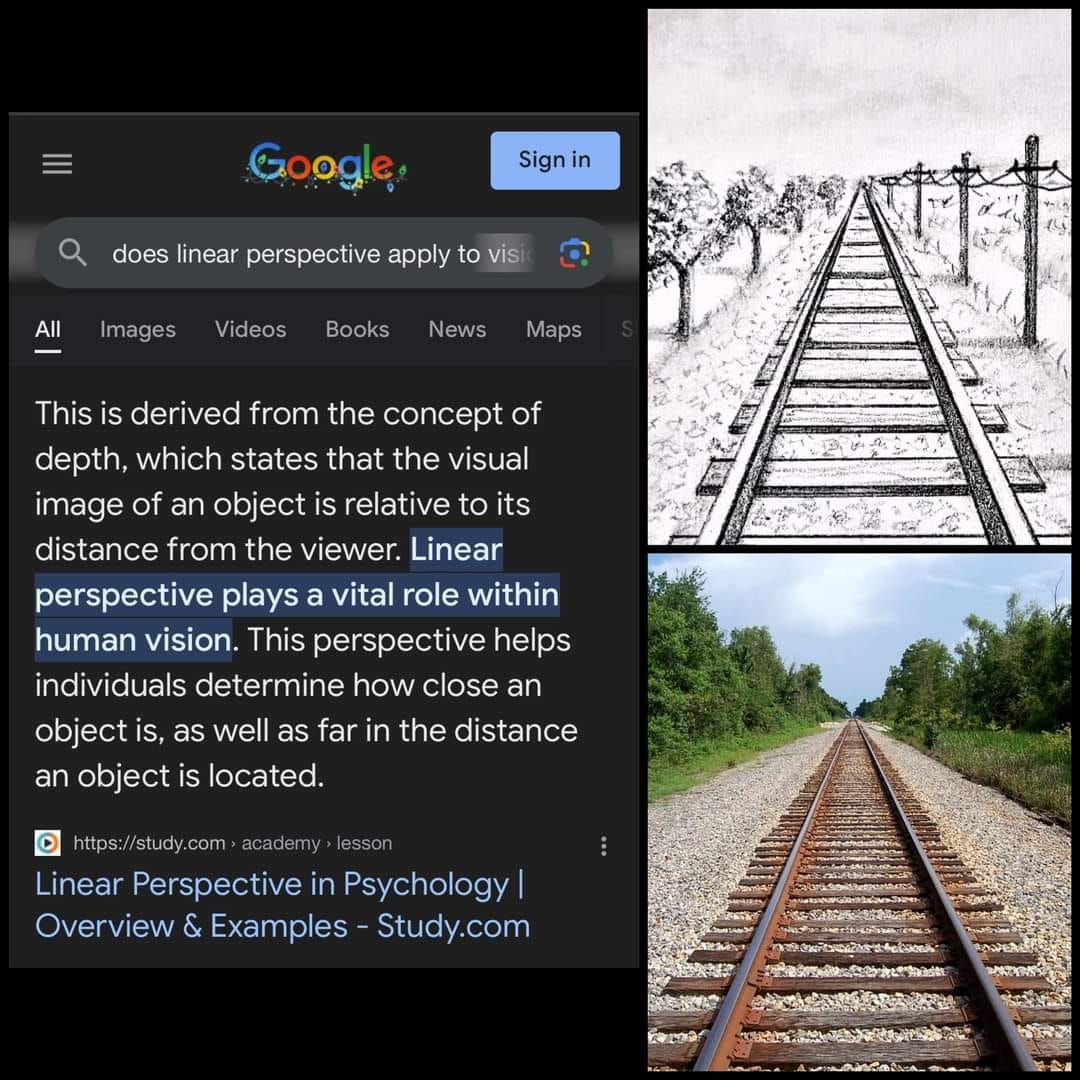
One factor, of several, that must be considered when viewing the Sun’s recession away from the observer is The Rayleigh Criterion. Among the many others factors include refraction, atmospheric distortion, and the apparent compression of objects on the horizon as they recede into the distance from the observer. The latter factor is revealed in the Laws of Perspective.
The human eye can only resolve objects as they move into the distance to a prescribed limit. Resolution limit describes how objects can appear to disappear and/or “blur out” into the distance, which is calculated using The Rayleigh Criterion. This is of particular importance when considering the apparent “setting” of The Sun over an imaginary curve, for The Rayleigh Criterion points out that before considering this apparent “setting” of the Sun, which is a Heliocentric claim, one must consider the role of the limitations of angular resolution, as they pertain to the naked human eye, as objects appear to disappear and/or “blur out” into the distance.
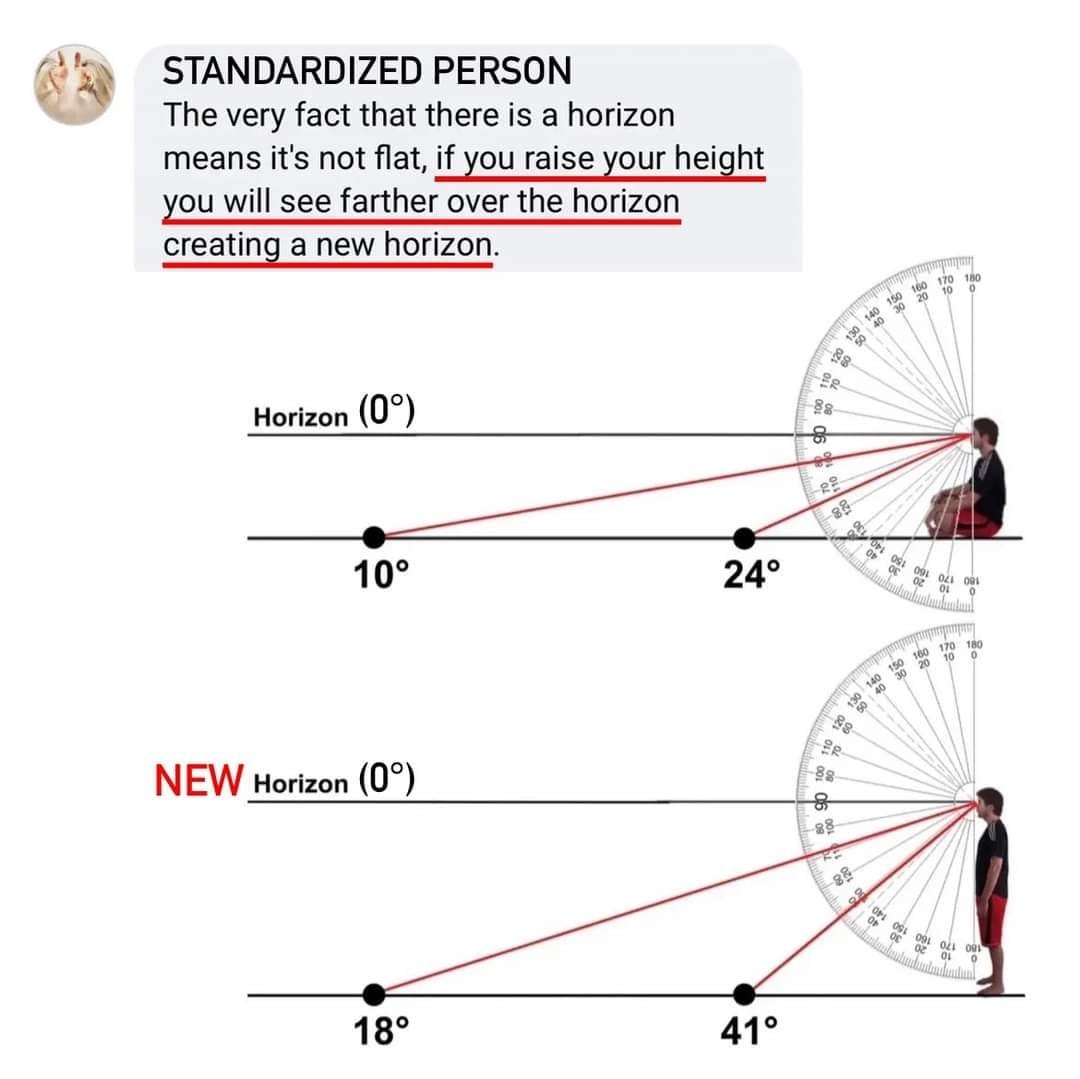
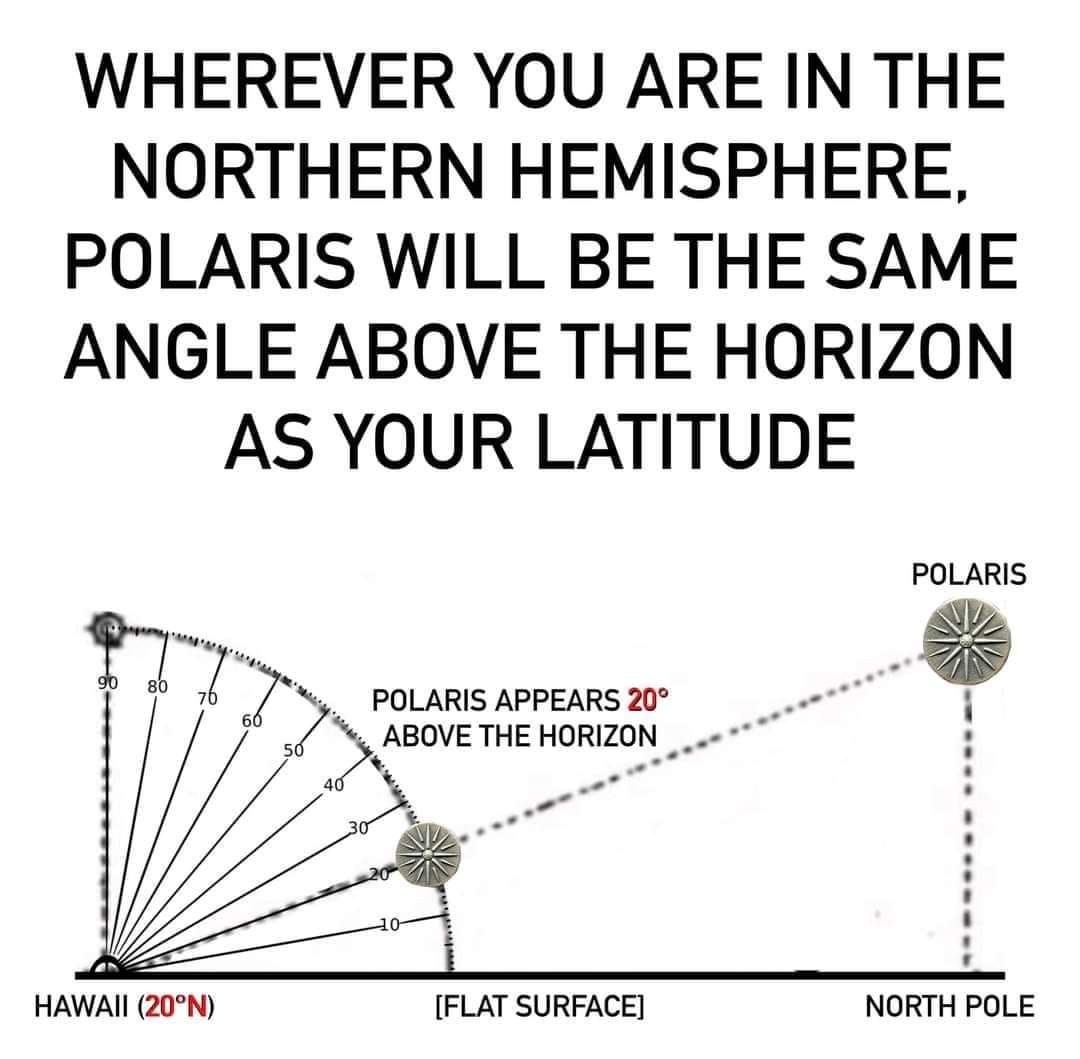
Angular Resolution and Horizons on Our Motionless Plane:
Angular Size Limit Ignored In Curve Maths Say Bob The Science Guy:
The Rayleigh Criterion:
When a point object is imaged using a circular aperture such as the lens or the iris of our eye, the image produced is not a point, rather a diffraction pattern. This is true, mainly when the size of the object is comparable to the wavelength of light.
A circular aperture creates a diffraction pattern of concentric rings that grow dimmer as we move away from the centre. These are known as Airy discs.
Because of the airy discs, point sources close to one another can overlap and produce a blurred image, as shown in the image.
To obtain a good image, point sources must be sufficiently far apart that their diffraction patterns do not overlap. To achieve this, the minimum distance between images must be such that the central maximum of the first image lies on the first minimum of the second and vice versa. Such an image is said to be just resolved. This is the famous Rayleigh criterion.
What is Rayleigh Criterion?
Consider the diffraction pattern for a circular aperture as shown in the figure below.
It can be shown that, for a circular aperture of diameter D, the first minimum in the diffraction pattern occurs at:
Θ=1.22λD
The accepted criterion for determining the diffraction limit to resolution based on this angle was developed by Lord Rayleigh in the 19th century:
“Rayleigh criterion for the diffraction limit to resolution states that two images are just resolvable when the centre of the diffraction pattern of one is directly over the first minimum of the diffraction pattern of the other.”
In the figure, the first minimum is at an angle:
Θ=1.22λD
So this means that two point objects are just resolvable if they are separated by an angle:
Θ=1.22λD
Rayleigh Criterion Solved Example
The Hubble Space Telescope’s primary mirror has a diameter of 2.40 m. (a) Determine the angle between two just-resolvable point light sources? Assume the average wavelength of light as 550 nm.
Solution:
The Rayleigh criterion gives the smallest possible angle 𝜃 between point sources.
Θ=1.22λD
Substituting the values in the above equation, we get:
Θ=1.22λD
Θ=1.22220×10−9m2.40m=2.80×10−7m
Resolving Power of Telescope
In telescopes, objects such as binary stars which are very close to each other, subtend small angles on the telescope. We need large apertures to resolve them. We can make use of Rayleigh’s Criterion to determine the resolving power of the telescope.
The angular separation between two objects must be:
Θ=1.22λD
Resolving power is defined as the inverse of the distance or angular separation between two objects which can be resolved through the optical instrument.
Therefore:
Resolving Power=1ΔΘ=d1.22λ
Thus, the higher the diameter d, the better the resolution. Astronomical optical telescopes have mirror diameters as large as 10 m to achieve the best resolution.
--https://byjus.com/physics/rayleigh-criterion/